Greninja (SSBU): Difference between revisions
(Undid edit by Cookies and Creme: u also gonna fite me) Tag: Undo |
m (Reverted edits by Thequantumharmonicoscillator (talk) to last version by Cookies and Creme.) Tag: Rollback |
||
| Line 1: | Line 1: | ||
{{ | {{ArticleIcons|ultimate=y}} | ||
{{ | {{disambig2|Greninja's appearance in ''Super Smash Bros. Ultimate''|the character in other contexts|Greninja}} | ||
{{Infobox Character | |||
|name = Greninja | |||
|image = [[File:Greninja SSBU.png|250px]] | |||
|game = SSBU | |||
|ssbgame1 = SSB4 | |||
|availability = [[Unlockable character|Unlockable]] | |||
}} | |||
'''Greninja''' ({{ja|ゲッコウガ|Gekkōga}}, ''Gekkouga'') is a playable character in ''[[Super Smash Bros. Ultimate]]''. It was officially revealed on June 12th, 2018 alongside {{SSBU|Mr. Game & Watch}} and the rest of the returning roster. Greninja is classified as [[Fighter number|Fighter #50]]. | |||
[[ | |||
Billy Bob Thompson, Yūji Ueda, Frédéric Clou and Benedikt Gutjan's portrayals of Greninja from ''Super Smash Bros. 4'' were repurposed for the English, Japanese, French and German versions of ''Ultimate'', respectively. | |||
==How to unlock== | |||
Complete one of the following: | |||
*Play [[VS. match]]es, with Greninja being the 58th character to be unlocked. | |||
*Clear {{SSBU|Classic Mode}} with {{SSBU|Donkey Kong}} or any character in his unlock tree, being the 6th character unlocked after {{SSBU|Sheik}}. | |||
*Have Greninja join the player's party in [[World of Light]]. | |||
Greninja must then be defeated on [[Kalos Pokémon League]] (the [[Ω form]] is used in World of Light). | |||
==Attributes== | |||
Greninja, true to being a ninja-themed character, has very strong mobility; it has the 8th fastest [[dash|run speed]], the 10th fastest [[air speed]], is tied for the 9th fastest [[fall speed|falling ]] (and [[fast fall|fast falling]]) speed, the 2nd highest [[gravity]], and possesses the 2nd highest [[jump|jump height]] overall. However, unlike most characters who boast similar mobility (such as {{SSBU|Sheik}}), Greninja boasts a surprising amount of KO options, good range on plenty of its attacks, and KO throws. | |||
One of Greninja's most notable traits is its high mobility which complements its grounded moveset. Greninja's dash attack comes out on frame 7 and has very low ending lag, as well as the ability to cross upon shields. Its knockback angle allows for many true follow-ups and strings over a large range of percents. Its neutral jab attack comes out on frame 3, making it a good grounded combo breaker. It can also lock, which gives Greninja access to potent punishes from opponents missing techs. Its down tilt is an excellent combo starter due to its low startup, ending lag and vertical launch angle. Greninja's up tilt is a frame 9 disjointed hitbox that acts well as an anti-air and can also be a combo starter. Its smash attacks are also reliable in their own right; its forward smash is quick for its range and power, down smash is an excellent punishment option for ledge regrabs, as well as sending at a low angle, and up smash is a potent combo finisher. | |||
Greninja also has a very strong air game due to its aforementioned air speed and jump height. Greninja's aerials are reliable for multiple situations and all have low landing lag (except for down aerial, at 30 frames). Its neutral aerial is a decent low percent combo starter due to it having incredibly low landing lag and a good launch angle. It can also KO at high percentages. Its forward aerial acts as a combo finisher from its combo starters and can KO moderately early. Forward aerial's low landing lag and disjointed nature also make it safe on shield in many situations when spaced correctly. Its up aerial is a great juggling option with low all-around lag and boasting good KO potential near the upper blast line. Greninja can also utilize its multihits to drag down opponents to create tech chase and jab lock situations. Its back aerial is a very fast follow up or offstage edgeguarding option. Down aerial can be used as a mix up to return to the stage from far above, as well as perform surprise combos on hit with both its [[meteor smash]] and sourspot hitbox. | |||
Greninja's grab game is overall very effective, due to its grabs being among the longest ranges of any non-tether grab in the game. Its forward, up, and back throws can KO at high percentages. Down throw acts as a middle percent combo starter, as well as a strong DI mix up, especially at higher percentages at ledge as a 50/50 between DI in and out in conjunction with forward throw. Up throw acts as a versatile combo starter that can lead to juggling situations. Because of this, Greninja has plenty of options off of a grab, as not one of its throws could be considered useless. | |||
and | Finally, Greninja's special moves are effective in various situations. [[Water Shuriken]] acts as a versatile zoning tool, as well as a high-percentage KO option when fully charged. At low-to-mid percents, it is also a combo starter, allowing Greninja to rush down its opponent and follow up with any aerial attack or an up smash. [[Shadow Sneak]] works as an effective recovery mix up, as well as a potent KO move from a good read or pseudo-combo finisher. Despite lacking an offensive hitbox, [[Hydro Pump]] is a good recovery move for its long distance, and can be used for gimping recoveries due to having windbox properties. [[Substitute]] is a counterattack with the unique attribute of being able to be aimed in one of 8 different directions upon a successful counter. These angled follow ups allow for Greninja to gain pseudo-follow ups as well as KO earlier by picking the optimal angle in regards to stage positioning. | ||
Like all characters, Greninja is flawed in many ways. One of Greninja's primary flaws is its inability to break out of disadvantage state. While not as bad as the previous game, Greninja still has difficulties escaping combos due to its fast falling speed and its aerials still having relatively high startup. This can sometimes be alleviated with its back or down aerials, but both are not very effective due to back aerial's almost entirely horizontal hitboxes and down aerial's landing lag. Another option is aerial Water Shuriken, which stalls Greninja in the air and can be used as a landing mix up, as well as Hydro Pump landing mix ups. | |||
Greninja's biggest weakness however, is its terrible out of shield game, which is arguably the worst of the entire cast. Because of its high short hop, its aerials slow startup, and lacking a fast grab (although it has good range), Greninja lacks an effective out of shield option faster than frame 14. While its back aerial is fairly quick at frame 5 (making it frame 8 out of shield), it is unable to hit opponents in front of Greninja and is very inconsistent at hitting opponents behind Greninja due to its high short hop. Jumping or rolling out of shield are potential options to reset neutral, but they are very predictable and easily read. Thus, when Greninja is pinned down in shield, it has difficulty escaping the situation without being heavily punished. Combined with its vulnerability to combos, this gives it an atrocious defensive game. | |||
the | Altogether, Greninja's playstyle requires players to think like an actual ninja: utilizing Greninja's superb mobility and fast attacks to rush down opponents, saving the slower attacks for potential mixups, mindgames and surprise KO options, and remaining unpredictable to prevent being trapped into disadvantageous positions. | ||
==Changes from ''[[Super Smash Bros. 4]]''== | |||
Greninja has been greatly buffed from ''Smash 4'' to ''Ultimate''. Its playstyle's traits have been further improved in the transition, while the general engine changes benefit said playstyle. | |||
Most of the universal changes notably benefit Greninja. As with all other characters in the game, Greninja's already quick mobility is faster like most characters, which benefits its hit-and-run playstyle, allowing Greninja to close in the distance and escape to reset the neutral game much more easily. The ability to run cancel into any ground move allows Greninja to further exploit its amazing ground mobility, allowing for easier setups into its combo starters, such as up and down tilt and dash attack. Furthermore, the reduced landing lag on Greninja's aerial attacks gives it an easier time landing, while the universal 3-frame jumpsquat improves Greninja's ground-to-air potential. The implementation of [[spot dodge]] canceling improves its potential punish game, due to its wide variety of combo starters and fast frame data. Finally, the changes to air dodge mechanics slightly improve its previously below average edgeguarding game. | |||
Aside from the universal changes, Greninja has also received notable direct buffs. The biggest ones were to its grab game: its standing grab is faster and its pummel, previously one of the worst in ''Smash 4'', deals less damage but is significantly faster, which allows Greninja to deal much more damage before throwing the opponent. Greninja's forward throw has higher knockback, allowing it to KO in an emergency, as with up throw. Its up and down throws also have better combo and juggling potential due to the universal changes to mobility - down throw notably now allows for potential KO confirms into forward and back aerial. Other buffs include [[Water Shuriken]] having more range, improving Greninja's camping ability. Greninja now has a new down tilt that has lower ending lag and sends at more favorable angles, and its dash attack sends at a higher angle, further improving Greninja's combo game. Greninja's KO power has also been buffed, with forward smash and forward aerial receiving higher knockback, up smash connecting better into its second hit, and down smash having faster startup. Lastly, [[Substitute]] now slows opponents down and offers Greninja intangibility during all of its attack variations, bringing it in line with other counterattacks. | |||
which | |||
On the other hand, Greninja is not without its nerfs. Notably, the ability to tech footstools has made footstool combos harder to pull off, which hinders Greninja's combo ability (specifically from its down aerial); however, this nerf is alleviated by Greninja's buffed combo game, due to other universal changes that impact it more positively. Substitute's attack variants are all weaker while also being more laggy overall, which compensates for the attack's new intangibility. In exchange for its buffed mobility, Greninja is now lighter, which brings it slightly more in-line with other combo-centric and/or hit-and-run characters, while not compensating much for its vulnerability to combos. | |||
As a result of receiving multiple buffs with relatively few nerfs, Greninja has improved significantly from ''Smash 4'', and has retained its status as a viable character in ''Ultimate'', with above average representation and some strong results in competitive play thanks to smashers such as {{Sm|iStudying}}, {{Sm|Jw}}, {{Sm|Lea}}, {{Sm|Somé}}, and {{Sm|Stroder}}. Because of this, Greninja is considered as a high or even top-tier character by many professional players. | |||
{{SSB4 to SSBU changelist|char=Greninja}} | |||
==Update history== | |||
Greninja has received a mix of minor buffs and nerfs via game updates. Several glitches have also been fixed over time. | |||
'''{{GameIcon|ssbu}} {{SSBU|1.2.0}}''' | |||
{{UpdateList (SSBU)/1.2.0|char=Greninja}} | |||
'''{{GameIcon|ssbu}} {{SSBU|2.0.0}}''' | |||
{{UpdateList (SSBU)/2.0.0|char=Greninja}} | |||
'''{{GameIcon|ssbu}} {{SSBU|3.0.0}}''' | |||
{{UpdateList (SSBU)/3.0.0|char=Greninja}} | |||
'''{{GameIcon|ssbu}} {{SSBU|3.1.0}}''' | |||
{{UpdateList (SSBU)/3.1.0|char=Greninja}} | |||
= | '''{{GameIcon|ssbu}} {{SSBU|4.0.0}}''' | ||
{{UpdateList (SSBU)/4.0.0|char=Greninja}} | |||
{{ | '''{{GameIcon|ssbu}} {{SSBU|7.0.0}}''' | ||
{{UpdateList (SSBU)/7.0.0|char=Greninja}} | |||
'''{{GameIcon|ssbu}} {{SSBU|8.0.0}}''' | |||
{{UpdateList (SSBU)/8.0.0|char=Greninja}} | |||
==Moveset== | |||
* Greninja can [[Crawling|crawl]], [[wall cling]], and [[wall jump]]. | |||
''For a gallery of Greninja's hitboxes, see [[Greninja (SSBU)/Hitboxes|here]].'' | |||
{{MovesetTable | |||
|neutralname= | |||
|neutralcount=3 | |||
|neutralinf=y | |||
|neutral1dmg=2% | |||
|neutral2dmg=2% | |||
|neutral3dmg=3% | |||
|neutralinfdmg=0.5% (loop), 2% (last) | |||
|neutraldesc=Two alternating palm thrusts followed by a double palm thrust that emits a small blast of water. If button mashed, it is instead followed by a series of knifehand strikes that emit blade-shaped water blasts that concludes with an outward knifehand strike that emits a wide blast of water. It can also be jab canceled, such as into forward tilt, down tilt and forward smash. | |||
|ftiltname= | |||
=== | |ftiltdmg=7.3% | ||
|ftiltdesc=A hook kick which stops half way. It can be angled and can [[lock]] opponents. | |||
| | |utiltname= | ||
| | |utiltdmg=4.5% | ||
| | |utiltdesc=Swings its tongue upwards. A good aerial combo starter and juggling tool due to its low knockback and somewhat disjointed hitbox. It can combo into itself at low percents and is a reliable way to connect into up aerial. | ||
| | |dtiltname= | ||
| | |dtiltdmg=4% | ||
|dtiltdesc=Does a downward hand sweep. It sends opponents at an upward angle, making it a versatile combo starter. Notably, it can confirm a KO into an up smash rather easily. | |||
|dashname= | |||
|dashdmg=8% | |||
|dashdesc=Does a sweep kick. Is arguably one of the best dash attacks in the game, as it launches opponents at an excellent angle for combos, making it one of Greninja's best combo starters. Reliably combos into back aerial at virtually any percent, and can set up up aerial strings or drag-down combos with up aerial. | |||
|fsmashname= | |||
|fsmashdmg=14% | |||
|fsmashdesc=An inward slash with a water kunai. Deals good knockback and has good range. However, it has notable ending lag. | |||
|usmashname= | |||
|usmashdmg=5% (hit 1), 14% (hit 2 clean center), 11% (hit 2 clean sides), 10% (hit 2 late) | |||
|usmashdesc=Two reverse gripped inward slashes with water kunai, similar to {{SSBU|Sheik}}'s up smash. Greninja's strongest finisher, especially when hit clean. Can be combo'd into from a down-tilt at specific percentages for a KO. | |||
|dsmashname= | |||
|dsmashdmg=13% (kunai), 11% (arms) | |||
|dsmashdesc=Hits both sides with water kunai. Due to it sending opponents at an [[semi-spike]] angle and coming out on frame 11, it is a quick and effective way to set up an edge-guard situation. | |||
|nairname= | |||
|nairdmg=11% (clean), 6% (late) | |||
|nairdesc=Strikes a ninjutsu pose while emitting an exploding water bubble. Despite noticeable start-up lag for a neutral aerial(frame 12), it boasts great combo potential at low to mid percentages with its strong and weak hits and can KO confirm into up-smash at high percents with the weak hit. It can also KO at very high percents with its strong hit. | |||
|fairname= | |||
|fairdmg=14% | |||
|fairdesc=Slashes with a water kunai. It has some start-up and suffers from high end lag, but it is a great tool in the neutral for spacing due to its disjointed hitbox and can be used for KOing. It is also safe on shield if spaced correctly. | |||
|bairname= | |||
|bairdmg= 3% (hit 1), 2.5% (hit 2), 6% (hit 3) | |||
|bairdesc=Kicks backwards three times. It is Greninja's fastest aerial attack, although it is also one of the weakest aerials of its kind. However, this makes it a useful combo tool in return, as it can be followed up from a down throw, down tilt, as well as a dash attack. It can be a situational out-of-shield option if the opponent crosses-up on its shield. | |||
|uairname= | |||
|uairdmg=1.3% (hits 1-5), 3% (hit 6) | |||
|uairdesc=Does a upward corkscrew kick, similar to both {{SSBU|Sheik}}'s and {{SSBU|Joker}}'s up aerials. One of Greninja's best combo and KO tools, as it can juggle and KO effectively due to its great jumping prowess. It also allows for drag-down combos because it's multi-hit properties, although this requires precise timing to land it at the right time, as its final launching hit comes out too fast to set up drag-down combos otherwise. | |||
|dairname= | |||
|dairdmg=8% | |||
|dairdesc=A diving double foot stomp. It acts as a [[stall-then-fall]] and bounces off opponents. The clean hit [[meteor smash]]es opponents while the late hit sends the opponent upwards, allowing for some situational combos. | |||
|grabname= | |||
|grabdesc=Grabs with a whirlpool. While its standing grab is slow, it is among the longest-reaching grabs in the game. | |||
|pummelname= | |||
|pummeldmg=1% | |||
|pummeldesc=Compresses target with water. Decent speed. | |||
|fthrowname= | |||
|fthrowdmg=3.5% (hit 1), 4.5% (throw) | |||
|fthrowdesc=Shoves the opponent forward. Can KO at high percentages near the edge. | |||
|bthrowname= | |||
|bthrowdmg=9% | |||
|bthrowdesc=Greninja leans forward and flings the opponent backwards. Like forward throw, its decent knockback gives it good edgeguarding potential at high percentages. | |||
|uthrowname= | |||
|uthrowdmg=5% | |||
|uthrowdesc=Tosses the opponent upwards. One of Greninja's most useful throws, as it can combo into a up tilt or up aerial at low and medium percents and can even KO at later percents. | |||
|dthrowname= | |||
|dthrowdmg=5% | |||
|dthrowdesc=Slams the opponent onto the ground. It can combo into a down tilt, forward tilt, and dash attack at low percentages. It can combo into back aerial at medium percents and later into forward aerial as well at higher percentages with good timing. | |||
|floorfname= | |||
|floorfdmg=8% | |||
|floorfdesc=Sweep kicks around itself while getting up. | |||
|floorbname= | |||
|floorbdmg=8% | |||
|floorbdesc=Sweep kicks around itself while getting up. | |||
|floortname= | |||
|floortdmg=8% | |||
|floortdesc=Sweep kicks around itself while getting up. | |||
|edgename= | |||
|edgedmg=9% | |||
|edgedesc=Performs a roundhouse kick while climbing up. | |||
|nsname=Water Shuriken | |||
|nsdmg=3%-10.8% (uncharged), 1.0% (fully charged looping hits), 9% (fully charged final hit) | |||
|nsdesc=Uses Water Shuriken, which can be charged. Depending on how long the move is charged, the shuriken will be larger and do more damage, however the speed and distance will decrease as a result. At full charge, it hits multiple times and can kill with a Shadow Sneak follow-up at low and medium percents. It is also a decent KOing option at higher percents. A fully charged water shuriken that is reflected at a higher speed will have trouble landing the final hit on Greninja because of the looping hits not moving Greninja far enough for it. | |||
|ssname=Shadow Sneak | |||
|ssdmg=10% (normal), 12% (reverse) | |||
|ssdesc=Disappears briefly, then preforms a forward kick or a drop kick (relative to the user's reappearance in relation to the enemy) to attack. The move activates when the special button is released. The way the shadow moves is relative to Greninja's position, and it can be moved further or closer to change how far Greninja teleports. While performing Shadow Sneak, Greninja cannot run, attack, grab, dodge or shield. However, it can walk slowly, jump and taunt. Has strong knockback and base knockback, which allows it to kill notably early when hitting the move offstage. | |||
|usname=Hydro Pump | |||
|usdmg=2% (per shot) | |||
|usdesc=Uses Hydro Pump to propel itself in the inputted direction; it can be used twice. Each shot has a [[windbox]] effect that pushes opponents, making it a decent option for gimping predictable recoveries. | |||
|dsname=Substitute | |||
|dsdmg=14% (up or down), 11% (left or right) | |||
|dsdesc=Does a pose, and if anyone hits it while posing, Greninja will temporarily disappear, get replaced by a wooden log or a Substitute doll, and then appear behind the opponent and strike them. It deviates noticeably from other counters, as the attack itself can be angled in an inputted direction and launching the opponent in that direction (with the down input meteor smashing opponents, which makes it a good punish against reckless edgeguarders). | |||
|fsname=Secret Ninja Attack | |||
|fsdmg=6% (the mat), 50% (Total in the attack after mat) | |||
|fsdesc=Turns into Ash-Greninja and attacks the opponent with a mat. If an opponent is caught in the mat, Greninja will send them up into the air and strike the opponent repeatedly in midair with its kunai, before slamming them down with a final hit. | |||
|game=SSBU | |||
|dtauntname= | |||
|dtauntdmg=0.5% | |||
|dtauntdesc=While standing on one foot, Greninja holds out its hands, faces the screen, and summons small sprays of water. The sprays produce some knockback, though they're able to KO only at above 420%. A video showing the exact KO percentages at which each character can be KO'd can be found [https://www.youtube.com/watch?v=cH7IDQ_8vic here]. Unlike the rest of Greninja's taunts, this one cannot be cancelled (unless Shadow Sneak is being charged before using it). | |||
}} | }} | ||
===[[On-screen appearance]]=== | |||
*Emerges from a [[Poké Ball]], then performs a ninjutsu hand sign that emits a small burst of water from its hands. | |||
<gallery> | |||
GreninjaOnScreenAppearanceSSBU.gif|Greninja's on-screen appearance | |||
</gallery> | |||
< | |||
===[[Taunt]]s=== | |||
*'''Up Taunt''': Stands upright, clasping its hands together before assuming a ninjutsu stance. The stance resembles one of its attack animations from the ''Pokémon'' series. | |||
*'''Side Taunt''': Shakes head from side to side, causing its tongue to whip out in the same directions. Particles of saliva fly off with each whip. | |||
*'''Down Taunt''': Poses with arms out and palms upward, and summons small sprays of water from them, which deal a small amount of damage. | |||
<gallery> | |||
SSBUGreninjaTaunt1.gif|Greninja's up taunt. | |||
SSBUGreninjaTaunt2.gif|Greninja's side taunt. | |||
SSBUGreninjaTaunt3.gif|Greninja's down taunt. | |||
</gallery> | |||
===[[Idle Pose]]s=== | |||
*Crosses arms over its body, then separates them with a flourish. | |||
*Hunches over and assumes a ninjutsu stance. | |||
< | <gallery> | ||
SSBUGreninjaIdle1.gif|Greninja's first idle pose | |||
SSBUGreninjaIdle2.gif|Greninja's second idle pose | |||
</gallery> | |||
===[[Crowd cheer]]=== | |||
< | <div class="tabber"> | ||
<div class="tabbertab" title="English, Japanese/Chinese, Italian, Dutch, French"> | |||
{| class="wikitable" border="1" cellpadding="4" cellspacing="1" | |||
|- | |||
!{{{name|}}} | |||
!Cheer (English) | |||
!Cheer (Japanese/Chinese) | |||
!Cheer (Italian) | |||
!Cheer (Dutch) | |||
!Cheer (French) | |||
|- | |||
! scope="row"|Cheer | |||
|[[File:Greninja Cheer English SSBU.ogg|center]]||[[File:Greninja Cheer Japanese SSBU.ogg|center]]||[[File:Greninja Cheer Italian SSBU.ogg|center]]||[[File:Greninja Cheer Dutch SSBU.ogg|center]]||{{NTSC}} [[File:Greninja Cheer French NTSC SSBU.ogg|center]] <br> {{PAL}} [[File:Greninja Cheer French PAL SSBU.ogg|center]] | |||
|- | |||
! scope="row"|Description | |||
|Gre - ninja! || Ge - kkou -ga! || Gre - nin - ja! || Gre - ninja! || Am - phi - no - bi! | |||
|} | |||
</div> | |||
<div class="tabbertab" title="German, Spanish, Russian, Korean"> | |||
{| class="wikitable" border="1" cellpadding="4" cellspacing="1" | |||
|- | |||
!{{{name|}}} | |||
!Cheer (German) | |||
!Cheer (Spanish) | |||
!Cheer (Russian) | |||
!Cheer (Korean) | |||
|- | |||
! scope="row"|Cheer | |||
|[[File:Greninja Cheer German SSBU.ogg|center]]||{{NTSC}} [[File:Greninja Cheer Spanish NTSC SSBU.ogg|center]] <br> {{PAL}} [[File:Greninja Cheer Spanish PAL SSBU.ogg|center]]||[[File:Greninja Cheer Russian SSBU.ogg|center]]||[[File:Greninja Cheer Korean SSBU.ogg|center]] | |||
|- | |||
! scope="row"|Description | |||
|Quaaaaa - jutsu! || Greninja! Greninja! Ya ya ya! || Gre - ninja! || Gae - gul - nin - ja! | |||
|} | |||
</div> | |||
</div> | |||
== | ===[[Victory pose]]s=== | ||
== | *'''Left:''' Does a few hand seals with splashing water, and then a ninja pose. It resembles one of its attack animations in [[bulbapedia:Pokémon X and Y|''Pokémon X'' and ''Y'']]. | ||
*'''Up:''' Performs Double Team to briefly create three afterimages of itself. | |||
*'''Right:''' Does a flip, lands in a spinning pose, and crosses its arms. | |||
[[File:PokemonSeriesVictoryThemeUltimate.ogg|thumb|A small excerpt of the title theme of ''Pokémon Red, Blue, Yellow, and Green Versions'', a track which would go on to become the ''Pokémon'' main theme and the title theme for the entire series.]] | |||
<gallery> | |||
GreninjaVictoryPose1SSBU.gif | |||
GreninjaVictoryPose2SSBU.gif | |||
GreninjaVictoryPose3SSBU.gif | |||
</gallery> | |||
==In competitive play== | |||
In the early metagame, players quickly noticed that Greninja had been buffed from ''Smash 4'', with improved versatility and speed and, despite losing its [[footstool]] combos, gained a stronger combo game thanks to improved frame data on moves such as dash attack, up throw, down throw, and neutral air. Despite this, Greninja is not a very popular pick due to its high learning curve. Nevertheless, smashers such as {{Sm|Stroder}}, {{Sm|Venia}}, {{Sm|Jw}}, and {{Sm|Lea}} have proven that the character is a very viable pick, and Greninja has been solidified as a upper high-tier character. | |||
===Most historically significant players=== | |||
<!--This character has a ten player limit for this section. Before adding and/or removing a player, read these guidelines: https://www.ssbwiki.com/SmashWiki:Notability#%22Most_historically_significant_players%22_guidelines --> | |||
''Any number following the Smasher name indicates placement on the [[Fall 2019 PGRU]], which recognizes the official top 50 players in the world in [[Super Smash Bros. Ultimate]] from July 13th, 2019 to December 15th, 2019.'' | |||
''See also: [[:Category:Greninja professionals (SSBU)]]'' | |||
The | *{{Sm|Elexiao|France}} - One of the best Greninja players in Europe. Placed 1st at {{Trn|4 Seasons Tournament: Winter 2020}}, 2nd at {{Trn|SEL 4: Crêpes Strikes Back}}, 5th at {{Trn|VCA 2019}}, 7th at {{Trn|Valhalla III}}, and 9th at {{Trn|Ultimate Fighting Arena 2019}} with wins over players such as {{Sm|Oryon}}, {{Sm|Flow}}, and {{Sm|Tru4}}. Currently ranked 13th on the [[European Smash Rankings]]. | ||
*{{Sm|iStudying|Netherlands}} - One of the best Greninja players in Europe. Placed 1st at both {{Trn|The Ultimate Performance 3}} and {{Trn|Heroes of Dutch Comic Con Winter Edition}}, 9th at both {{Trn|Ultimate Fighting Arena 2019}} and {{Trn|Temple: Hermès Edition}}, and 13th at {{Trn|Valhalla III}} with wins over players such as {{Sm|Stroder Ame}}, {{Sm|quiK}}, and {{Sm|Space}}. Currently ranked 15th on the [[European Smash Rankings]]. | |||
*{{Sm|Jw|Canada}} - The best Greninja player in Canada. Placed 9th at {{Trn|Pound 2019}}, 13th at {{Trn|Shine 2019}}, 17th at both {{Trn|Get On My Level 2019}} and {{Trn|The Big House 9}}, and 33rd at {{Trn|Frostbite 2020}} with wins over players such as {{Sm|MkLeo}}, {{Sm|Mr. E}}, and {{Sm|Wishes}}. Currently ranked 1st on the [[Smash Canada Rankings Ultimate]]. | |||
*{{Sm|Lea|Japan}} (#21) - The best Greninja player in the world. Placed 5th at both {{Trn|Umebura SP 3}} and {{Trn|Umebura SP 6}}, 7th at both {{Trn|2GG: Kongo Saga}} and {{Trn|Kagaribi 4}}, and 9th at {{Trn|Frostbite 2019}} with wins over players such as {{Sm|KEN}}, {{Sm|Raito}}, and {{Sm|Dabuz}}. | |||
*{{Sm|Oisiitofu|Japan}} - Placed 9th at both {{Trn|Sumabato SP 2}} and {{Trn|Maesuma TOP 1}}, 13th at {{Trn|Sumabato SP 12}}, and 17th at both {{Trn|KVOxTSB 2019}} and {{Trn|Sumabato SP 7}} with wins over players such as {{Sm|Zackray}}, {{Sm|Atelier}}, and {{Sm|Nishiya}}. Currently ranked 86th on the [[Japan Player Rankings]]. | |||
*{{Sm|Regerets|Philippines}} - The best Greninja player in the Philippines. Placed 3rd at {{Trn|Gamebookr's Mid-Year Smash Tournament}} and 7th at both {{Trn|Uprising 2019}} and {{Trn|REV Major 2019}} with wins over players such as {{Sm|Aluf}}, {{Sm|JJROCKETS}}, and {{Sm|PSI Force}}. Currently ranked 1st on the [[Filipino Power Rankings]]. | |||
*{{Sm|Somé|Japan}} - Placed 1st at {{Trn|TSC 11}}, 3rd at {{Trn|TSC 12}}, 7th at {{Trn|Sumabato SP 4}}, 9th at {{Trn|Umebura SP 6}}, and 13th at {{Trn|Umebura SP 4}} with wins over players such as {{Sm|Jagaimo}}, {{Sm|Etsuji}}, and {{Sm|HIKARU}}. Currently ranked 21st on the [[Japan Player Rankings]]. | |||
*{{Sm|Stroder|USA}} - One of the best Greninja players in the world. Placed 1st at {{Trn|Ascension VIII}}, 5th at {{Trn|Glitch 8 - Missingno}}, 9th at {{Trn|Mainstage}}, 13th at {{Trn|Shine 2019}}, and 25th at {{Trn|EVO 2019}} with wins over players such as {{Sm|Tweek}}, {{Sm|Maister}}, and {{Sm|ESAM}}. Formerly ranked 29th on the [[Spring 2019 PGRU]]. | |||
*{{Sm|Tarik|Germany}} - One of the best Greninja players in Europe. Placed 1st at {{Trn|Calyptus Cup X: Powwer Up}}, 2nd at {{Trn|Smashwick 4}}, 7th at {{Trn|Syndicate 2019}}, 9th at {{Trn|Ultimate Fighting Arena 2019}}, and 25th at {{Trn|Glitch 8 - Missingno}} with wins over players such as {{Sm|ESAM}}, {{Sm|MVD}}, and {{Sm|Chag}}. Ranked 14th on the [[European Smash Rankings]]. | |||
*{{Sm|Venia|USA}} - One of the best Greninja players in the United States but is currently banned from several tournaments. Placed 3rd at both {{Trn|Player's Ball Ultimate}} and {{Trn|Return to Yoshi's Island}}, 25th at {{Trn|Let's Make Big Moves}}, and 33rd at both {{Trn|The Big House 9}} and {{Trn|GENESIS 7}} with wins over {{Sm|Tweek}}, {{Sm|Dabuz}}, and {{Sm|Mr. E}}. Currently ranked 2nd on the [[New York City Power Rankings#Super Smash Bros. Ultimate rankings|New York City Ultimate Power Rankings]]. | |||
=={{SSBU|Classic Mode}}: Your Turn, Greninja!== | |||
[[File:SSBU Congratulations Greninja.png|thumb|Greninja's congratulations screen.]] | |||
Greninja fights against characters that represent different types from the ''Pokémon'' games: for example, Charizard and Bowser represent the Fire type, while Mewtwo, Ness and Lucas represent the Psychic type. | |||
{|class="wikitable" style="text-align:center" | |||
!Round!!Opponent!!Stage!!Music!!Notes | |||
|- | |||
|1||{{CharHead|Charizard|SSBU|hsize=20px}} and {{CharHead|Bowser|SSBU|hsize=20px}}||[[Pokémon Stadium]]||''{{SSBUMusicLink|Pokémon|Battle! (Elite Four) / Battle! (Solgaleo/Lunala)}}''||Represents Fire-type. Charizard's {{SSBU|Pokémon Trainer}} is absent. | |||
|- | |||
|2||{{CharHead|Pikachu|SSBU|hsize=20px}}, {{CharHead|Pichu|SSBU|hsize=20px}}, and {{CharHead|Zero Suit Samus|SSBU|hsize=20px}}||[[Pokémon Stadium 2]]||''{{SSBUMusicLink|Pokémon|Battle! (Steven)}}''||Represents Electric-type. | |||
|- | |||
|3||{{CharHead|Lucario|SSBU|hsize=20px}}, {{CharHead|Ryu|SSBU|hsize=20px}}, and {{CharHead|Ken|SSBU|hsize=20px}}||Pokémon Stadium||''{{SSBUMusicLink|Pokémon|Battle! (Reshiram / Zekrom)}}''||Represents Fighting-type. | |||
< | |- | ||
|4||{{CharHead|Ivysaur|SSBU|hsize=20px}}||Pokémon Stadium||''{{SSBUMusicLink|Pokémon|Battle! (Gladion)}}''||Represents Grass-type. Ivysaur's Pokémon Trainer is absent. | |||
|- | |||
|5||{{CharHead|Mewtwo|SSBU|hsize=20px}}, {{CharHead|Ness|SSBU|hsize=20px}}, and {{CharHead|Lucas|SSBU|hsize=20px}}||Pokémon Stadium 2||''{{SSBUMusicLink|Pokémon|Battle! (Dialga/Palkia) / Spear Pillar}}''||Represents Psychic-type. | |||
|- | |||
|6||{{CharHead|Squirtle|SSBU|hsize=20px}} and {{Head|Greninja|g=SSBU|s=20px|cl=Black}} Greninja||[[Kalos Pokémon League]]||''{{SSBUMusicLink|Pokémon|Battle! (Champion) - Pokémon X / Pokémon Y}}''||Represents Water-type. Squirtle's Pokémon Trainer is absent. The CPU will be the {{Head|Greninja|g=SSBU|s=20px}} default Greninja if the player chooses the black costume. | |||
|- | |||
|colspan="5"|[[Bonus Stage]] | |||
|- | |||
|Final||{{SSBU|Master Hand}}||{{SSBU|Final Destination}}||''{{SSBUMusicLink|Super Smash Bros.|Master Hand}}'' <small>(Less than 7.0 intensity)</small><br>''{{SSBUMusicLink|Super Smash Bros.|Master Hand / Crazy Hand}}'' <small>(Intensity 7.0 or higher)</small>||On intensity 7.0 and higher, {{SSBU|Crazy Hand}} fights alongside Master Hand. | |||
|} | |||
The | Note: All rounds except the sixth round take place on Pokémon Stadium and Pokémon Stadium 2. If applicable, each stage will also shift to their appropriately-typed form at the earliest possible opportunity. (The stages remain in their default form in rounds 3 and 5, as none of the stages have Psychic or Fighting-themed forms.) | ||
[[Credits]] roll after completing Classic Mode. Completing it as Greninja has ''{{SSBUMusicLink|Pokémon|Battle! (Trainer Battle) - Pokémon X / Pokémon Y}}'' accompany the credits. | |||
{{clr}} | |||
==Role in [[World of Light]]== | |||
[[File:WoL-50Greninja.jpg|thumb|Finding Greninja in World of Light|left]] | |||
Greninja was among the fighters that were summoned to fight the army of [[Master Hand]]s. | |||
During the opening cutscene, Greninja was present on the cliffside when [[Galeem]] unleashed his beams of light. Greninja leaped into the air to avoid one of the beams, which hit {{SSBU|Lucario}} instead. Greninja was hit shortly after and vaporized, getting imprisoned by Galeem afterward along with the other fighters, sans {{SSBU|Kirby}}. A puppet fighter cloned from Greninja is later seen alongside ones cloned from {{SSBU|Fox}}, {{SSBU|Samus}}, {{SSBU|Link}} and other fighters. | |||
Greninja was one of the many fighters that fell under [[Dharkon]]'s control upon Galeem's first defeat, and it can be found in the [[Mysterious Dimension]] at [[The Dark Realm]]. It can be seen impeding the path, making it an obligatory unlock. | |||
Greninja is later seen among several other fighters, making their last stand against Galeem and Dharkon. It also shows up in the bad ending where Galeem emerges victorious against Dharkon, witnessing Galeem engulf the world in light. | |||
{{clrl}} | |||
===Fighter Battle=== | |||
< | {|class="wikitable" style="width:100%;" | ||
|- | |||
!style="width:5%;"|No. | |||
!style="width:5%;"|Image | |||
!Name | |||
!Type | |||
!Power | |||
!Stage | |||
!Music | |||
|- | |||
|50 | |||
|[[File:Greninja SSBU.png|center|64x64px]] | |||
|Greninja | |||
|{{SpiritType|Shield}} <center>{{color|#18aef5|Shield}}</center> | |||
|10,600 | |||
|[[Kalos Pokémon League]] ([[Ω form]]) | |||
|''{{SSBUMusicLink|Pokémon|Battle! (Trainer Battle) - Pokémon X / Pokémon Y}}'' | |||
|} | |||
{{clear}} | |||
==[[Spirit]]== | |||
Greninja's fighter spirit can be obtained by completing {{SSBU|Classic Mode}}. It is also available periodically for purchase in the shop for 300 Gold, but only after Greninja has been unlocked. Unlocking Greninja in World of Light allows the player to preview the spirit below in the Spirit List under the name "???". As a fighter spirit, it cannot be used in Spirit Battles and is purely aesthetic. Its fighter spirit has an alternate version that replaces it with its artwork in ''Ultimate''. | |||
<center> | |||
<gallery> | |||
SSBU spirit Greninja.png|418. '''''Greninja''''' | |||
</gallery> | |||
</center> | |||
In the | ==In Spirit battles== | ||
===As the main opponent=== | |||
{|class="wikitable sortable" style="width:100%;" | |||
! colspan=4|Spirit | |||
! colspan=7|Battle parameters | |||
! colspan=1|Inspiration | |||
|- | |||
! style="width:5%;"|No. | |||
! style="width:5%;"|Image | |||
! Name | |||
! Series | |||
! Enemy Fighter(s) | |||
! style="width:5%;"|Type | |||
! style="width:5%;"|Power | |||
! Stage | |||
! Rules | |||
! Conditions | |||
! Music | |||
! Character | |||
|- | |||
|154 | |||
|{{SpiritTableName|Winky|size=64}} | |||
|''Donkey Kong'' Series | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}} | |||
|{{SpiritType|Attack}} | |||
|1,700 | |||
|[[Mushroom Kingdom U]] | |||
|N/A | |||
|•The enemy deals damage when falling<br>•The enemy has increased jump power | |||
|{{SSBUMusicLink|Donkey Kong|Jungle Level (Brawl)}} | |||
| | |||
|- | |||
|199 | |||
|{{SpiritTableName|Zora|size=64}} | |||
|''The Legend of Zelda'' Series | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Violet}} | |||
|{{SpiritType|Shield}} | |||
|1,800 | |||
|[[Great Bay]] | |||
|N/A | |||
|•The enemy's neutral special has increased power | |||
|{{SSBUMusicLink|The Legend of Zelda|Ocarina of Time Medley}} | |||
| | |||
|- | |||
|385 | |||
|{{SpiritTableName|Slippy Toad|link=y|size=64}} | |||
|''Star Fox'' Series | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}}<br>•{{SSBU|Fox}} {{Head|Fox|g=SSBU|s=20px|cl=Black}} | |||
|{{SpiritType|Shield}} | |||
|9,600 | |||
|[[Frigate Orpheon]] (hazards off) | |||
|N/A | |||
|•Defeat the main fighter to win<br>•Timed battle (1:30)<br>•The enemy tends to avoid conflict | |||
|{{SSBUMusicLink|Star Fox|Corneria - Star Fox}} | |||
| | |||
|- | |||
|482 | |||
|{{SpiritTableName|Raikou, Entei, & Suicune|customname=[[Raikou]], [[Entei]], & [[Suicune]]|size=64}} | |||
|''Pokémon'' Series | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Violet}}<br>•{{SSBU|Incineroar}} {{Head|Incineroar|g=SSBU|s=20px|cl=White}}<br>•{{SSBU|Pikachu}} {{Head|Pikachu|g=SSBU|s=20px|cl=Libre}} | |||
|{{SpiritType|Shield}} | |||
|9,900 | |||
|[[Suzaku Castle]] | |||
|•Hazard: Lava Floor | |||
|•The floor is lava | |||
|{{SSBUMusicLink|Pokémon|Pokémon Red / Pokémon Blue Medley}} | |||
|Suicune | |||
|- | |||
|516 | |||
|{{SpiritTableName|Darkrai|link=y|size=64}} | |||
|''Pokémon'' Series | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Black}} | |||
|{{SpiritType|Shield}} | |||
|9,900 | |||
|[[Luigi's Mansion]] ([[Ω form]]) | |||
|•Item: [[Black Hole]]<br>•Hazard: Slumber Floor | |||
|•The floor is sleep-inducing<br>•Only certain Pokémon will emerge from Poké Balls (Darkrai) | |||
|{{SSBUMusicLink|Pokémon|Battle! (Team Galactic)}} | |||
| | |||
|- | |||
|770 | |||
|{{SpiritTableName|Metal Gear RAY|size=64}} | |||
|''Metal Gear Solid'' Series | |||
|•Metal {{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Grey}} (140 HP) | |||
|{{SpiritType|Grab}} | |||
|4,200 | |||
|[[Shadow Moses Island]] | |||
|•Item: Exploding Types | |||
|•[[Stamina battle]]<br>•Explosion attacks aren't as effective against the enemy<br>•The enemy is metal | |||
|{{SSBUMusicLink|Metal Gear|Yell "Dead Cell"}} | |||
| | |||
|- | |||
|893 | |||
|{{SpiritTableName|Shadow Man|size=64}} | |||
|''Mega Man'' Series | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Purple}}×3 (60 HP) | |||
|{{SpiritType|Shield}} | |||
|3,500 | |||
|[[Norfair]] ([[Battlefield form]]) | |||
|N/A | |||
|•The enemy's neutral special has increased power<br>•[[Stamina battle]]<br>•The enemy favors neutral specials | |||
|{{SSBUMusicLink|Mega Man|Shadow Man Stage}} | |||
| | |||
|- | |||
|1,014 | |||
|{{SpiritTableName|Luka|size=64}} | |||
|''Bayonetta'' Series | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Black}} | |||
|{{SpiritType|Shield}} | |||
|3,800 | |||
|[[New Donk City Hall]] | |||
|•Temporary Invincibility | |||
|•The enemy becomes temporarily invincible when badly damaged | |||
|{{SSBUMusicLink|Bayonetta|Riders Of The Light}} | |||
| | |||
|- | |||
|1,048 | |||
|{{SpiritTableName|Octoling Octopus|size=64}} | |||
|''Splatoon'' Series | |||
|•{{SSBU|Greninja}} Team {{Head|Greninja|g=SSBU|s=20px|cl=Pink}}×4 | |||
|{{SpiritType|Shield}} | |||
|3,900 | |||
|[[Moray Towers]] | |||
|N/A | |||
|•Timed battle (2:00) | |||
|{{SSBUMusicLink|Splatoon|Octoweaponry}} | |||
| | |||
|- | |||
|1,143 | |||
|{{SpiritTableName|Frog & Snake|customname=[[Sablé Prince|Frog & Snake]]|size=64}} | |||
|''Kaeru no Tame ni Kane wa Naru'' | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}}<br>•{{SSBU|King K. Rool}} {{Head|King K. Rool|g=SSBU|s=20px|cl=Blue}} | |||
|{{SpiritType|Shield}} | |||
|3,600 | |||
|[[Dream Land GB]] (Castle Lololo interior) | |||
|•Assist Trophy Enemies ([[Sablé Prince]]) | |||
|•Hostile assist trophies will appear | |||
|{{SSBUMusicLink|Kirby|Kirby Retro Medley}} (Castle Lololo) | |||
|Frog | |||
|- | |||
|rowspan="2"|1,291 | |||
|{{SpiritTableName|Ninjara|link=y|size=64|dlcalt=y}} | |||
|rowspan="2"|''ARMS'' | |||
|•{{SSBU|Greninja}} {{Head|Greninja|g=SSBU|s=20px|cl=Green}} | |||
|rowspan="2"|{{SpiritType|Grab}} | |||
|rowspan="2"|3,600 | |||
|rowspan="2"|[[Suzaku Castle]] | |||
|rowspan="2"|•Item: [[Boomerang]] | |||
|rowspan="2"|•The enemy has increased move speed | |||
|rowspan="2"|{{SSBUMusicLink|ARMS|Ninja College}} | |||
|rowspan="2"| | |||
|- | |||
|style="background-color:#EEE;"|•{{SSBU|Mii Brawler}} {{Head|Mii Brawler|g=SSBU|s=20px}} (Moveset [[Flashing Mach Punch|2]][[Suplex|3]][[Soaring Axe Kick|1]][[Counter Throw|3]], Ninjara Wig, Ninjara Outfit)<ref group="SB" name="DLC"/> | |||
|} | |||
<references group="SB"> | |||
<ref name="DLC">This alternative occurs when the corresponding DLC has been purchased and downloaded.</ref> | |||
</references> | |||
== | ==[[Alternate costume (SSBU)#Greninja|Alternate costumes]]== | ||
{ | {|style="margin:1em auto 1em auto;text-align:center" | ||
|- | |||
|colspan=8|[[File:Greninja Palette (SSBU).png|link=Alternate costume (SSBU)#Greninja|1000px]] | |||
|- | |||
|{{Head|Greninja|g=SSBU|s=50px}} | |||
|{{Head|Greninja|g=SSBU|s=50px|cl=Red}} | |||
|{{Head|Greninja|g=SSBU|s=50px|cl=Pink}} | |||
|{{Head|Greninja|g=SSBU|s=50px|cl=Black}} | |||
|{{Head|Greninja|g=SSBU|s=50px|cl=Violet}} | |||
|{{Head|Greninja|g=SSBU|s=50px|cl=Green}} | |||
{{ | |{{Head|Greninja|g=SSBU|s=50px|cl=Grey}} | ||
|{{Head|Greninja|g=SSBU|s=50px|cl=Purple}} | |||
|} | |||
== | ==Gallery== | ||
{{ | <gallery> | ||
Pokémon Smash Bros.png|Artwork of all playable Pokémon characters and Poké Ball Pokémon, as posted by the official Pokémon Twitter account. | |||
SSBU Greninja Number.png|Greninja's fighter card. | |||
Greninja unlock notice SSBU.jpg|Greninja's unlock notice. | |||
SSBUWebsiteGreninja1.jpg|Greninja coming to a halt on [[Kalos Pokémon League]]. | |||
SSBUWebsiteGreninja2.jpg|Charging [[Water Shuriken]] next to {{SSBU|Ryu}} on [[Suzaku Castle]]. | |||
SSBUWebsiteGreninja3.jpg|Jumping on {{SSBU|Battlefield}}. | |||
SSBUWebsiteGreninja4.jpg|Performing its neutral aerial with [[Leviathan]] on [[Midgar]]. | |||
SSBUWebsiteGreninja5.jpg|With its [[Substitute|Substitute Doll]] on [[Wuhu Island]] after [[tripping]]. | |||
SSBUWebsiteGreninja6.jpg|Performing [[Shadow Sneak]] on [[Luigi's Mansion]]. | |||
SSBUWebsiteLucario3.jpg|Struck by {{SSBU|Lucario}} on [[Pokémon Stadium 2]]. | |||
</gallery> | |||
== | ===Fighter Showcase Video=== | ||
{{#widget:YouTube|id=rMCn8NuATaE}} | |||
{{ | ==Trivia== | ||
*In the ''Pokémon'' series, Ash-Greninja is only obtainable as a male. The fact that Greninja transforms into Ash-Greninja for its [[Final Smash]], [[Secret Ninja Attack]], implies that Greninja is a male in ''Ultimate''. | |||
*Greninja's new character portrait resembles its [[air dodge]] animation. | |||
**It also resembles {{SSB4|Fox}}'s character portrait from ''Super Smash Bros. 4'' but with the arm and leg positions mirrored. | |||
*Greninja's fighter number, 50, is the same as the number of its [[mariowiki:Costume Mario|costume]] in ''Super Mario Maker''. It shares this distinction with {{SSBU|Inkling}}. | |||
*Greninja, {{SSBU|Ivysaur}}, {{SSBU|Olimar}}, {{SSBU|Little Mac}}, {{SSBU|Ryu}} and {{SSBU|Ken}} are the only characters to never appear as minions in any Spirit battles. | |||
*Alongside {{SSBU|Luigi}}, Greninja is one of two characters in ''Ultimate'' with a taunt that cannot be cancelled, due to the fact that their non-cancelable taunts have hitboxes. | |||
**Strangely, this does not apply for {{SSBU|Snake}} and {{SSBU|Kazuya}}'s taunts that have damaging hitboxes | |||
**Greninja and Luigi are also the only two characters whose Classic Mode titles feature their names. | |||
*Greninja can also be unlocked immediately after clearing Classic Mode as Sheik, referencing their ninja-like traits and movements. | |||
*Greninja appears slightly tilted in its [[damage meter]] compared to its character artwork. This distinction is shared with fellow ''Pokémon'' series character {{SSBU|Incineroar}}. | |||
**Coincidentally, both are final evolutions of starter Pokémon and both have Dark as their secondary type. | |||
**Both are also found and unlocked in the Dark Realm in World of Light. | |||
*Incineroar and {{SSBU|Jigglypuff}} are the only Pokémon that are not encountered in Greninja's Classic Mode route. | |||
*Oddly, Greninja does not vanish when performing a directional [[air dodge]] despite the sound effects playing. It shares this oddity with {{SSBU|Rosalina & Luma}} and {{SSBU|Palutena}}. | |||
*In ''Ultimate'', Greninja has a weight of 88, which almost matches its weight in ''Pokémon'' (in pounds), being 88.2 lbs. | |||
{{ | {{SSBUCharacters}} | ||
[[Category: | {{Pokémon universe}} | ||
[[Category: | [[Category:Greninja (SSBU)| ]] | ||
[[Category: | [[Category:Pokémon (SSBU)]] | ||
[[Category:Spirits]] | |||
[[es:Greninja (SSBU)]] | |||
Revision as of 10:02, February 9, 2022
| Greninja in Super Smash Bros. Ultimate | |
|---|---|
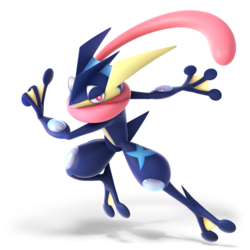 
| |
| Universe | Pokémon |
| Other playable appearance | in SSB4 |
| Availability | Unlockable |
| Final Smash | Secret Ninja Attack |
Greninja (ゲッコウガ, Gekkouga) is a playable character in Super Smash Bros. Ultimate. It was officially revealed on June 12th, 2018 alongside Mr. Game & Watch and the rest of the returning roster. Greninja is classified as Fighter #50.
Billy Bob Thompson, Yūji Ueda, Frédéric Clou and Benedikt Gutjan's portrayals of Greninja from Super Smash Bros. 4 were repurposed for the English, Japanese, French and German versions of Ultimate, respectively.
How to unlock
Complete one of the following:
- Play VS. matches, with Greninja being the 58th character to be unlocked.
- Clear Classic Mode with Donkey Kong or any character in his unlock tree, being the 6th character unlocked after Sheik.
- Have Greninja join the player's party in World of Light.
Greninja must then be defeated on Kalos Pokémon League (the Ω form is used in World of Light).
Attributes
Greninja, true to being a ninja-themed character, has very strong mobility; it has the 8th fastest run speed, the 10th fastest air speed, is tied for the 9th fastest falling (and fast falling) speed, the 2nd highest gravity, and possesses the 2nd highest jump height overall. However, unlike most characters who boast similar mobility (such as Sheik), Greninja boasts a surprising amount of KO options, good range on plenty of its attacks, and KO throws.
One of Greninja's most notable traits is its high mobility which complements its grounded moveset. Greninja's dash attack comes out on frame 7 and has very low ending lag, as well as the ability to cross upon shields. Its knockback angle allows for many true follow-ups and strings over a large range of percents. Its neutral jab attack comes out on frame 3, making it a good grounded combo breaker. It can also lock, which gives Greninja access to potent punishes from opponents missing techs. Its down tilt is an excellent combo starter due to its low startup, ending lag and vertical launch angle. Greninja's up tilt is a frame 9 disjointed hitbox that acts well as an anti-air and can also be a combo starter. Its smash attacks are also reliable in their own right; its forward smash is quick for its range and power, down smash is an excellent punishment option for ledge regrabs, as well as sending at a low angle, and up smash is a potent combo finisher.
Greninja also has a very strong air game due to its aforementioned air speed and jump height. Greninja's aerials are reliable for multiple situations and all have low landing lag (except for down aerial, at 30 frames). Its neutral aerial is a decent low percent combo starter due to it having incredibly low landing lag and a good launch angle. It can also KO at high percentages. Its forward aerial acts as a combo finisher from its combo starters and can KO moderately early. Forward aerial's low landing lag and disjointed nature also make it safe on shield in many situations when spaced correctly. Its up aerial is a great juggling option with low all-around lag and boasting good KO potential near the upper blast line. Greninja can also utilize its multihits to drag down opponents to create tech chase and jab lock situations. Its back aerial is a very fast follow up or offstage edgeguarding option. Down aerial can be used as a mix up to return to the stage from far above, as well as perform surprise combos on hit with both its meteor smash and sourspot hitbox.
Greninja's grab game is overall very effective, due to its grabs being among the longest ranges of any non-tether grab in the game. Its forward, up, and back throws can KO at high percentages. Down throw acts as a middle percent combo starter, as well as a strong DI mix up, especially at higher percentages at ledge as a 50/50 between DI in and out in conjunction with forward throw. Up throw acts as a versatile combo starter that can lead to juggling situations. Because of this, Greninja has plenty of options off of a grab, as not one of its throws could be considered useless.
Finally, Greninja's special moves are effective in various situations. Water Shuriken acts as a versatile zoning tool, as well as a high-percentage KO option when fully charged. At low-to-mid percents, it is also a combo starter, allowing Greninja to rush down its opponent and follow up with any aerial attack or an up smash. Shadow Sneak works as an effective recovery mix up, as well as a potent KO move from a good read or pseudo-combo finisher. Despite lacking an offensive hitbox, Hydro Pump is a good recovery move for its long distance, and can be used for gimping recoveries due to having windbox properties. Substitute is a counterattack with the unique attribute of being able to be aimed in one of 8 different directions upon a successful counter. These angled follow ups allow for Greninja to gain pseudo-follow ups as well as KO earlier by picking the optimal angle in regards to stage positioning.
Like all characters, Greninja is flawed in many ways. One of Greninja's primary flaws is its inability to break out of disadvantage state. While not as bad as the previous game, Greninja still has difficulties escaping combos due to its fast falling speed and its aerials still having relatively high startup. This can sometimes be alleviated with its back or down aerials, but both are not very effective due to back aerial's almost entirely horizontal hitboxes and down aerial's landing lag. Another option is aerial Water Shuriken, which stalls Greninja in the air and can be used as a landing mix up, as well as Hydro Pump landing mix ups.
Greninja's biggest weakness however, is its terrible out of shield game, which is arguably the worst of the entire cast. Because of its high short hop, its aerials slow startup, and lacking a fast grab (although it has good range), Greninja lacks an effective out of shield option faster than frame 14. While its back aerial is fairly quick at frame 5 (making it frame 8 out of shield), it is unable to hit opponents in front of Greninja and is very inconsistent at hitting opponents behind Greninja due to its high short hop. Jumping or rolling out of shield are potential options to reset neutral, but they are very predictable and easily read. Thus, when Greninja is pinned down in shield, it has difficulty escaping the situation without being heavily punished. Combined with its vulnerability to combos, this gives it an atrocious defensive game.
Altogether, Greninja's playstyle requires players to think like an actual ninja: utilizing Greninja's superb mobility and fast attacks to rush down opponents, saving the slower attacks for potential mixups, mindgames and surprise KO options, and remaining unpredictable to prevent being trapped into disadvantageous positions.
Changes from Super Smash Bros. 4
Greninja has been greatly buffed from Smash 4 to Ultimate. Its playstyle's traits have been further improved in the transition, while the general engine changes benefit said playstyle.
Most of the universal changes notably benefit Greninja. As with all other characters in the game, Greninja's already quick mobility is faster like most characters, which benefits its hit-and-run playstyle, allowing Greninja to close in the distance and escape to reset the neutral game much more easily. The ability to run cancel into any ground move allows Greninja to further exploit its amazing ground mobility, allowing for easier setups into its combo starters, such as up and down tilt and dash attack. Furthermore, the reduced landing lag on Greninja's aerial attacks gives it an easier time landing, while the universal 3-frame jumpsquat improves Greninja's ground-to-air potential. The implementation of spot dodge canceling improves its potential punish game, due to its wide variety of combo starters and fast frame data. Finally, the changes to air dodge mechanics slightly improve its previously below average edgeguarding game.
Aside from the universal changes, Greninja has also received notable direct buffs. The biggest ones were to its grab game: its standing grab is faster and its pummel, previously one of the worst in Smash 4, deals less damage but is significantly faster, which allows Greninja to deal much more damage before throwing the opponent. Greninja's forward throw has higher knockback, allowing it to KO in an emergency, as with up throw. Its up and down throws also have better combo and juggling potential due to the universal changes to mobility - down throw notably now allows for potential KO confirms into forward and back aerial. Other buffs include Water Shuriken having more range, improving Greninja's camping ability. Greninja now has a new down tilt that has lower ending lag and sends at more favorable angles, and its dash attack sends at a higher angle, further improving Greninja's combo game. Greninja's KO power has also been buffed, with forward smash and forward aerial receiving higher knockback, up smash connecting better into its second hit, and down smash having faster startup. Lastly, Substitute now slows opponents down and offers Greninja intangibility during all of its attack variations, bringing it in line with other counterattacks.
On the other hand, Greninja is not without its nerfs. Notably, the ability to tech footstools has made footstool combos harder to pull off, which hinders Greninja's combo ability (specifically from its down aerial); however, this nerf is alleviated by Greninja's buffed combo game, due to other universal changes that impact it more positively. Substitute's attack variants are all weaker while also being more laggy overall, which compensates for the attack's new intangibility. In exchange for its buffed mobility, Greninja is now lighter, which brings it slightly more in-line with other combo-centric and/or hit-and-run characters, while not compensating much for its vulnerability to combos.
As a result of receiving multiple buffs with relatively few nerfs, Greninja has improved significantly from Smash 4, and has retained its status as a viable character in Ultimate, with above average representation and some strong results in competitive play thanks to smashers such as iStudying, Jw, Lea, Somé, and Stroder. Because of this, Greninja is considered as a high or even top-tier character by many professional players.
Aesthetics
 Greninja's model features a slightly more subdued color scheme, more closely resembling its appearance in recent mainline Pokémon games. Its body and tongue appear to have a glossy, wet sheen. The textures on Greninja's tongue have also been adjusted.
Greninja's model features a slightly more subdued color scheme, more closely resembling its appearance in recent mainline Pokémon games. Its body and tongue appear to have a glossy, wet sheen. The textures on Greninja's tongue have also been adjusted. Greninja is slightly more expressive, squinting akin to how it does in the Pokémon anime in a few of his animations.
Greninja is slightly more expressive, squinting akin to how it does in the Pokémon anime in a few of his animations. Every move that once used water katanas now uses water kunai, similar to when Ash's Greninja uses Cut in the Pokémon anime.
Every move that once used water katanas now uses water kunai, similar to when Ash's Greninja uses Cut in the Pokémon anime. Greninja's tongue has less physics-based movement than the previous game.
Greninja's tongue has less physics-based movement than the previous game. Greninja has altered animations for its sidestep, roll, and airdodge animations; it now disappears in a small whirlwind with leaves scattering, similarly to when Substitute is successful.
Greninja has altered animations for its sidestep, roll, and airdodge animations; it now disappears in a small whirlwind with leaves scattering, similarly to when Substitute is successful. Greninja's victory pose where it flips in the air and lands with its arms crossed has been altered: the camera doesn't move as much, causing Greninja's body to face away from the camera.
Greninja's victory pose where it flips in the air and lands with its arms crossed has been altered: the camera doesn't move as much, causing Greninja's body to face away from the camera.
Attributes
 Like all characters, Greninja's jumpsquat animation takes 3 frames to complete (down from 4).
Like all characters, Greninja's jumpsquat animation takes 3 frames to complete (down from 4). Greninja walks faster (1.43 → 1.502).
Greninja walks faster (1.43 → 1.502). Greninja dashes faster (2.08 → 2.288).
Greninja dashes faster (2.08 → 2.288).
 Its initial dash is significantly faster (1.6 → 2.178).
Its initial dash is significantly faster (1.6 → 2.178).
 Greninja's air speed is faster (1.18 → 1.239).
Greninja's air speed is faster (1.18 → 1.239). Greninja is lighter (94 → 88), worsening its survivability.
Greninja is lighter (94 → 88), worsening its survivability. Greninja's traction is higher (0.045 → 0.087).
Greninja's traction is higher (0.045 → 0.087). Forward roll has less ending lag (FAF 30 → 29).
Forward roll has less ending lag (FAF 30 → 29). Back roll grants more intangibility (frames 4-14 → 4-15).
Back roll grants more intangibility (frames 4-14 → 4-15). Back roll has more ending lag (FAF 33 → 34).
Back roll has more ending lag (FAF 33 → 34). Spot dodge has less ending lag (FAF 26 → 25).
Spot dodge has less ending lag (FAF 26 → 25). Spot dodge has more startup with less intangibility (frames 2-16 → 3-16).
Spot dodge has more startup with less intangibility (frames 2-16 → 3-16). Air dodge grants more intangibility (frames 2-26 → 2-27).
Air dodge grants more intangibility (frames 2-26 → 2-27). Air dodge has significantly more ending lag (FAF 32 → 42).
Air dodge has significantly more ending lag (FAF 32 → 42). The changes to locking and the ability to tech aerial footstools hurts Greninja more than the rest of the cast, weakening notorious damage racking and KO setups it possessed in Smash 4.
The changes to locking and the ability to tech aerial footstools hurts Greninja more than the rest of the cast, weakening notorious damage racking and KO setups it possessed in Smash 4. The increased shieldstun, shield grab startup and shield drop lag further hinder Greninja's poor out of shield game, now being arguably the worst out of the cast, as unlike most other characters, all its options that can bypass shield drop lag are either too slow or, in the case of its back aerial, cannot hit most opponents on the ground.
The increased shieldstun, shield grab startup and shield drop lag further hinder Greninja's poor out of shield game, now being arguably the worst out of the cast, as unlike most other characters, all its options that can bypass shield drop lag are either too slow or, in the case of its back aerial, cannot hit most opponents on the ground.
Ground attacks
- Neutral attack:
 The first two hits have lower knockback (hit 1: 30 base/30 scaling → 20 / 25/25/15/15; hit 2: 30 base/50 scaling → 20/ 25/25/20), and keep opponents on the ground (hit 1: 70°/60°/80° → 361°/361°/180°/361°; hit 2: 70°/60°/90° → 361°). This allows them to connect better and jab lock.
The first two hits have lower knockback (hit 1: 30 base/30 scaling → 20 / 25/25/15/15; hit 2: 30 base/50 scaling → 20/ 25/25/20), and keep opponents on the ground (hit 1: 70°/60°/80° → 361°/361°/180°/361°; hit 2: 70°/60°/90° → 361°). This allows them to connect better and jab lock. The first three hits have smaller hitboxes overall (hit 1: 3u/2.5u/3.5u → 2.0u/2.0u/2.2u/2.2u; hit 2: 3u/2.5u/4u → 2.5u/2.8u/3.0u; hit 3: 5u/3u/3u → 3u/3.4u/4u). This reduces their vertical range.
The first three hits have smaller hitboxes overall (hit 1: 3u/2.5u/3.5u → 2.0u/2.0u/2.2u/2.2u; hit 2: 3u/2.5u/4u → 2.5u/2.8u/3.0u; hit 3: 5u/3u/3u → 3u/3.4u/4u). This reduces their vertical range. The second hit deals more damage (1.6% → 2%).
The second hit deals more damage (1.6% → 2%). The third hit deals less damage (3.5% → 3%), and thus less knockback.
The third hit deals less damage (3.5% → 3%), and thus less knockback. The third hit uses stationary hitboxes rather than hitboxes connected to Greninja's arms.
The third hit uses stationary hitboxes rather than hitboxes connected to Greninja's arms. The infinite has faster startup (frame 6 → 4), a shorter gap between hits (4 frames → 3), and has reduced knockback scaling (40 → 10) while gaining a hitstun modifier of 2 on each hit, allowing it to connect much more reliably.
The infinite has faster startup (frame 6 → 4), a shorter gap between hits (4 frames → 3), and has reduced knockback scaling (40 → 10) while gaining a hitstun modifier of 2 on each hit, allowing it to connect much more reliably. The infinite has a lower hitlag multiplier (1× → 0.5×) and SDI multiplier (1.1× → 0.4×), making it harder to escape.
The infinite has a lower hitlag multiplier (1× → 0.5×) and SDI multiplier (1.1× → 0.4×), making it harder to escape. The infinite is comprised of one extended hitbox rather than two normal ones (size: 5.2u/6.2u → 5.5; Y/Z-offset: 7/7 → 7.5/7.5; Z-stretch: 13 → 14).
The infinite is comprised of one extended hitbox rather than two normal ones (size: 5.2u/6.2u → 5.5; Y/Z-offset: 7/7 → 7.5/7.5; Z-stretch: 13 → 14). The infinite has gained a shieldstun multiplier of 4×. This allows it to lock opponents into their shields between each hit, and thus pressure them more effectively, but also allows them to cancel shieldstun and punish Greninja more easily if they shield 10 hits or more.
The infinite has gained a shieldstun multiplier of 4×. This allows it to lock opponents into their shields between each hit, and thus pressure them more effectively, but also allows them to cancel shieldstun and punish Greninja more easily if they shield 10 hits or more. The infinite's finisher has three hitboxes instead of two, with different sizes (5.6u/6.6 → 4.2u/4.2u/4.8u) and positions (ID 0: 7 Y-offset/8 Z-offset → 7.5/9; ID 1: 7 Y-offset/16 Z-offset → 7.3/13 → ID 2: 7.5 Y-offset/16.5 Z-offset. This increases its horizontal range, but lowers its vertical range.
The infinite's finisher has three hitboxes instead of two, with different sizes (5.6u/6.6 → 4.2u/4.2u/4.8u) and positions (ID 0: 7 Y-offset/8 Z-offset → 7.5/9; ID 1: 7 Y-offset/16 Z-offset → 7.3/13 → ID 2: 7.5 Y-offset/16.5 Z-offset. This increases its horizontal range, but lowers its vertical range. The infinite's finisher has reduced hitlag (3× → 2×).
The infinite's finisher has reduced hitlag (3× → 2×).
- Forward tilt:
 It deals more damage when angled (7.3% → 8.3%).
It deals more damage when angled (7.3% → 8.3%). It has significantly altered knockback (angled up: 20/30/40 base / 110/90/70 scaling → 50 / 100/79/58; non-angled/angled down: 20/30/40 base / 110/90/70 scaling → 50 / 98/77/56).
It has significantly altered knockback (angled up: 20/30/40 base / 110/90/70 scaling → 50 / 100/79/58; non-angled/angled down: 20/30/40 base / 110/90/70 scaling → 50 / 98/77/56).
 This improves its KO power if sweetspotted, especially when angled up, allowing it to KO middleweights at around 170% from center stage.
This improves its KO power if sweetspotted, especially when angled up, allowing it to KO middleweights at around 170% from center stage. However, this hinders its KO power if sourspotted, and removes its ability to lock opponents at low percents.
However, this hinders its KO power if sourspotted, and removes its ability to lock opponents at low percents.
- Down tilt:
 Greninja has a new down tilt: a downward hand sweep instead of a shin kick.
Greninja has a new down tilt: a downward hand sweep instead of a shin kick. It has less ending lag (FAF 27 → 23).
It has less ending lag (FAF 27 → 23). It has altered knockback (60 base/40 scaling → 30/110). This slightly narrows its combo range at low percentages, but increases it from mid to higher ones, to the point it now allows for KO confirms at high percents.
It has altered knockback (60 base/40 scaling → 30/110). This slightly narrows its combo range at low percentages, but increases it from mid to higher ones, to the point it now allows for KO confirms at high percents. It launches opponents at a more upward angle (70° → 79°/77°/75°), further improving its combo potential at high percents.
It launches opponents at a more upward angle (70° → 79°/77°/75°), further improving its combo potential at high percents. It deals less damage (7% → 4%).
It deals less damage (7% → 4%). It has smaller hitboxes (4u/3.5u/3u → 3u/2.5u/3u), reducing its vertical range.
It has smaller hitboxes (4u/3.5u/3u → 3u/2.5u/3u), reducing its vertical range.
- Dash attack:
 The move has an altered animation with Greninja stopping halfway through the spin.
The move has an altered animation with Greninja stopping halfway through the spin. It deals more damage (7% → 8%), with base knockback compensated (100 → 90).
It deals more damage (7% → 8%), with base knockback compensated (100 → 90). It has a longer hitbox duration (frames 7-10 → 7-11) and less ending lag (FAF 31 → 29).
It has a longer hitbox duration (frames 7-10 → 7-11) and less ending lag (FAF 31 → 29). It sends at a higher angle (60° → 70°). Combined with its lower ending lag and base knockback, this improves its combo ability.
It sends at a higher angle (60° → 70°). Combined with its lower ending lag and base knockback, this improves its combo ability.
- Forward smash:
 It deals more knockback (30 base/101 scaling → 35/104).
It deals more knockback (30 base/101 scaling → 35/104).
- Up smash:
 The first hit has a new hitbox that only hits grounded opponents with significantly reduced knockback (30 base/120 scaling → 20/10) and SDI multiplier (1× → 0.5×), whereas the previous hitbox can now only hit aerial opponents and has reduced knockback scaling (120 → 90). This makes the first hit connect more consistently into the second hit, no longer failing against opponents on platforms above Greninja.
The first hit has a new hitbox that only hits grounded opponents with significantly reduced knockback (30 base/120 scaling → 20/10) and SDI multiplier (1× → 0.5×), whereas the previous hitbox can now only hit aerial opponents and has reduced knockback scaling (120 → 90). This makes the first hit connect more consistently into the second hit, no longer failing against opponents on platforms above Greninja.
- Down smash:
 The move has much less startup lag (frame 16 → 11), with its total duration reduced as well (FAF 55 → 50).
The move has much less startup lag (frame 16 → 11), with its total duration reduced as well (FAF 55 → 50). The arms' hitboxes have been extended towards Greninja (Z-stretch: 0 → 7), and the move has one additional hitbox at each side during the last active frame, removing its blindspots.
The arms' hitboxes have been extended towards Greninja (Z-stretch: 0 → 7), and the move has one additional hitbox at each side during the last active frame, removing its blindspots.
Aerial attacks
 All aerials have less landing lag (12 frames → 7 (neutral), 15 → 11 (forward), 13 → 10 (back), 15 → 14 (up), 32 → 30 (down)).
All aerials have less landing lag (12 frames → 7 (neutral), 15 → 11 (forward), 13 → 10 (back), 15 → 14 (up), 32 → 30 (down)).- Neutral aerial:
 The move has considerably less ending lag (FAF 65 → 53), making it much less likely to cause a self-destruct offstage.
The move has considerably less ending lag (FAF 65 → 53), making it much less likely to cause a self-destruct offstage. The late hit has a longer duration (frames 14-16 → 14-19).
The late hit has a longer duration (frames 14-16 → 14-19).
- Forward aerial:
 It has much more knockback scaling (84 → 95), allowing it to KO roughly 20% earlier.
It has much more knockback scaling (84 → 95), allowing it to KO roughly 20% earlier. The move has a new, smaller extended hitbox directly in front of Greninja (size: 3u; Y/Z-offset: 7.5/8; Y-stretch: 8.5), removing its blindspot.
The move has a new, smaller extended hitbox directly in front of Greninja (size: 3u; Y/Z-offset: 7.5/8; Y-stretch: 8.5), removing its blindspot. The move's two other hitboxes are smaller (5.4u/4.4u → 4.7u/3.7u), and one of them is offset further from Greninja (Y-offset: -7 → -8), creating a new blindspot between them.
The move's two other hitboxes are smaller (5.4u/4.4u → 4.7u/3.7u), and one of them is offset further from Greninja (Y-offset: -7 → -8), creating a new blindspot between them.
- Back aerial:
 The move has less ending lag (FAF 46 → 41).
The move has less ending lag (FAF 46 → 41). It has bigger hitboxes (hits 1 and 2: 5u/4u/2u → 5.5u/4.3u/2.5u; hit 3: 5.8u/4.5u/2u → 5.8u/4.5u/2.5u).
It has bigger hitboxes (hits 1 and 2: 5u/4u/2u → 5.5u/4.3u/2.5u; hit 3: 5.8u/4.5u/2u → 5.8u/4.5u/2.5u). The last two hits have less startup (hit 2: frame 8 → 7; hit 3: frame 13 → 11).
The last two hits have less startup (hit 2: frame 8 → 7; hit 3: frame 13 → 11). The first hit sends at different angles, one of them being a different autolink angle (365°/30°/30° → 367°/35°/35°). This allows it to connect better into the second hit.
The first hit sends at different angles, one of them being a different autolink angle (365°/30°/30° → 367°/35°/35°). This allows it to connect better into the second hit. The third hit deals more damage (4% → 6%), with its knockback scaling not fully compensated (120 → 95), allowing it to KO slightly earlier.
The third hit deals more damage (4% → 6%), with its knockback scaling not fully compensated (120 → 95), allowing it to KO slightly earlier.
- Up aerial:
 The fifth hit uses the autolink angle like the previous hits (85° → 367°), allowing it to connect more reliably into the final hit, and increasing the move's window for drag-down setups.
The fifth hit uses the autolink angle like the previous hits (85° → 367°), allowing it to connect more reliably into the final hit, and increasing the move's window for drag-down setups. The first five hits have more base knockback (45 → 55), and the fifth hit no longer uses set knockback. This is overall beneficial to the move, as it inflicts more hitstun to opponents that further facilitates drag-down setups, without drastically disrupting its linking ability due to using the autolink angle.
The first five hits have more base knockback (45 → 55), and the fifth hit no longer uses set knockback. This is overall beneficial to the move, as it inflicts more hitstun to opponents that further facilitates drag-down setups, without drastically disrupting its linking ability due to using the autolink angle.
- Down aerial:
 The move has less ending lag if it misses (FAF 57 → 52), making it slightly safer to use offstage.
The move has less ending lag if it misses (FAF 57 → 52), making it slightly safer to use offstage. Greninja no longer loses its double jump when hitting with the move.
Greninja no longer loses its double jump when hitting with the move. It has more ending lag when it hits an opponent (FAF 13 → 21), hindering its combo potential and making it less safe on shield.
It has more ending lag when it hits an opponent (FAF 13 → 21), hindering its combo potential and making it less safe on shield. Its hitboxes are smaller (clean: 6u → 4.3u; late: 7u → 5.2u) and higher up (Y-offset: -2 → 0.1), reducing its range.
Its hitboxes are smaller (clean: 6u → 4.3u; late: 7u → 5.2u) and higher up (Y-offset: -2 → 0.1), reducing its range.
Throws and other attacks
- Grab:
 All grabs have more ending lag (standing: FAF 30 → 39; dash: 40 → 47; pivot: 36 → 42).
All grabs have more ending lag (standing: FAF 30 → 39; dash: 40 → 47; pivot: 36 → 42). Standing and pivot grab have one frame faster startup (standing: frame 11 → 10; pivot: frame 15 → 14).
Standing and pivot grab have one frame faster startup (standing: frame 11 → 10; pivot: frame 15 → 14). Dash grab has slower startup (frame 9 → 13).
Dash grab has slower startup (frame 9 → 13). Dash grab's grabbox doesn't extend out as far (Z-stretch: 20 → 17.5), reducing its range.
Dash grab's grabbox doesn't extend out as far (Z-stretch: 20 → 17.5), reducing its range. Pivot grab's grabbox extends further (Z-stretch: -22 → -25.3), increasing its range. It is now the largest non-tether pivot grab in the game.
Pivot grab's grabbox extends further (Z-stretch: -22 → -25.3), increasing its range. It is now the largest non-tether pivot grab in the game.
- Pummel:
 Pummel deals more hitlag (4 frames → 11), but has less startup (frame 6 → 2) and significantly ending lag (FAF 27 → 8). It is now one of the fastest pummels in the game, rather than one of the slowest.
Pummel deals more hitlag (4 frames → 11), but has less startup (frame 6 → 2) and significantly ending lag (FAF 27 → 8). It is now one of the fastest pummels in the game, rather than one of the slowest. It deals less damage (2% → 1%).
It deals less damage (2% → 1%).
 The speed of Greninja's forward, back, and up throws is no longer weight-dependent. This improves up throw's combo potential against heavyweights, but worsens it against lightweights.
The speed of Greninja's forward, back, and up throws is no longer weight-dependent. This improves up throw's combo potential against heavyweights, but worsens it against lightweights.- Forward throw:
 The move has gained a hitbox before the throw, increasing its damage (5% → 3.5% (hit 1), 4.5% (throw); 8% total) and allowing it to hit bystanders.
The move has gained a hitbox before the throw, increasing its damage (5% → 3.5% (hit 1), 4.5% (throw); 8% total) and allowing it to hit bystanders. It launches at a lower angle (50° → 40°) with much more knockback overall (70 base/45 scaling → 65/100), to the point it has above-average knockback for a forward throw rather than being one of the weakest in the game, greatly improving its utility for setting up edgeguards and KOing at very high percents.
It launches at a lower angle (50° → 40°) with much more knockback overall (70 base/45 scaling → 65/100), to the point it has above-average knockback for a forward throw rather than being one of the weakest in the game, greatly improving its utility for setting up edgeguards and KOing at very high percents.
- Back throw:
 Back throw deals more damage (8% → 9%).
Back throw deals more damage (8% → 9%). It has an altered animation: Greninja turns towards the screen instead of remaining facing forward, and swings its arms horizontally towards its back to toss the opponent.
It has an altered animation: Greninja turns towards the screen instead of remaining facing forward, and swings its arms horizontally towards its back to toss the opponent.
- Up throw:
 Up throw has one frame less ending lag (FAF 44 → 43).
Up throw has one frame less ending lag (FAF 44 → 43).
- Down throw:
 Down throw has less ending lag (FAF 43 → 38), improving its combo potential.
Down throw has less ending lag (FAF 43 → 38), improving its combo potential.
- Edge attack:
 Edge attack deals more damage (7% → 9%).
Edge attack deals more damage (7% → 9%).
- Down taunt:
 Down taunt has much more ending lag (FAF 80 → 110), further reducing its very limited utility.
Down taunt has much more ending lag (FAF 80 → 110), further reducing its very limited utility. Greninja now suffers hitlag when down taunt connects, but the opponent only suffers hitlag on the ground, as the air only hitboxes are flinchless, and thus cannot inflict hitlag. This effectively reduces the move's hit rate.
Greninja now suffers hitlag when down taunt connects, but the opponent only suffers hitlag on the ground, as the air only hitboxes are flinchless, and thus cannot inflict hitlag. This effectively reduces the move's hit rate.
Special moves
- Water Shuriken:
 Fully charged Water Shuriken travels faster (1.9 → 2.2), and has a longer maximum lifespan (32 frames → 36), significantly increasing its range to the point where it now has slightly more range than the uncharged version, rather than the other way around.
Fully charged Water Shuriken travels faster (1.9 → 2.2), and has a longer maximum lifespan (32 frames → 36), significantly increasing its range to the point where it now has slightly more range than the uncharged version, rather than the other way around. Opponents don't fall out of the fully charged shuriken as much as before.
Opponents don't fall out of the fully charged shuriken as much as before. Uncharged Water Shuriken has less knockback scaling (85 → 45).
Uncharged Water Shuriken has less knockback scaling (85 → 45). Water Shuriken looks sharper.
Water Shuriken looks sharper.
- Shadow Sneak:
 It can now be used multiple times in midair.
It can now be used multiple times in midair. Shadow Sneak's shadow travels faster.
Shadow Sneak's shadow travels faster. Both attack variants have less startup.
Both attack variants have less startup. Forward Shadow Sneak has a new animation: it is a forward kick instead of a handstand kick. It launches at a much lower angle (48° → 36°), improving its KO potential.
Forward Shadow Sneak has a new animation: it is a forward kick instead of a handstand kick. It launches at a much lower angle (48° → 36°), improving its KO potential. Greninja now cloaks itself in a whirlwind before disappearing.
Greninja now cloaks itself in a whirlwind before disappearing. Shadow Sneak stalls less in the air (initial vertical boost: 2.1 → 1.8), hindering its recovery usage.
Shadow Sneak stalls less in the air (initial vertical boost: 2.1 → 1.8), hindering its recovery usage. The shadow is notably darker, and the shadow's eyes flash red just before release. This makes it easier to predict the attack.
The shadow is notably darker, and the shadow's eyes flash red just before release. This makes it easier to predict the attack.
- Hydro Pump:
 Hydro Pump now has an arrow pointing in the direction of travel, similar to Pikachu's Quick Attack and Pichu's Agility.
Hydro Pump now has an arrow pointing in the direction of travel, similar to Pikachu's Quick Attack and Pichu's Agility. Hydro Pump can now be ledge-cancelled.
Hydro Pump can now be ledge-cancelled. Greninja no longer loses its double jump if it is hit out of Hydro Pump.
Greninja no longer loses its double jump if it is hit out of Hydro Pump. The water shots have considerably reduced knockback (65 (base)/100(scaling) → 60/80), and smaller hitboxes (6u → 4.7u), greatly reducing the move's offensive utility.
The water shots have considerably reduced knockback (65 (base)/100(scaling) → 60/80), and smaller hitboxes (6u → 4.7u), greatly reducing the move's offensive utility.
- Substitute:
 The counter window is longer (frames 8-29 → 8-34).
The counter window is longer (frames 8-29 → 8-34). It has more ending lag if it misses (FAF 65 → 70).
It has more ending lag if it misses (FAF 65 → 70). Substitute slows down the opponent when the attack activates, allowing the attack to land more consistently.
Substitute slows down the opponent when the attack activates, allowing the attack to land more consistently. All of the attack's variants have one frame faster startup (frame 41 → 40).
All of the attack's variants have one frame faster startup (frame 41 → 40). All of the attack's variants now grant Greninja intangibility during the attack (frames 1-37 → 1-56).
All of the attack's variants now grant Greninja intangibility during the attack (frames 1-37 → 1-56). All of the attack's variants have slightly more ending lag (FAF 85 → 87).
All of the attack's variants have slightly more ending lag (FAF 85 → 87). The side variant has much less knockback scaling (100 → 85).
The side variant has much less knockback scaling (100 → 85). The up and diagonal up variants deal less damage (up: 14% → 13%; diagonal up: 13% → 12%) and have less knockback scaling (both: 100 → 95), noticeably hindering their KO power.
The up and diagonal up variants deal less damage (up: 14% → 13%; diagonal up: 13% → 12%) and have less knockback scaling (both: 100 → 95), noticeably hindering their KO power. The down variant deals less damage (14% → 13%) and has less knockback (grounded: 100 scaling → 95; aerial: 50 base/100 scaling → 25/65). This hinders its KO power; particularly, the aerial version is no longer among the strongest meteor smashes in the game.
The down variant deals less damage (14% → 13%) and has less knockback (grounded: 100 scaling → 95; aerial: 50 base/100 scaling → 25/65). This hinders its KO power; particularly, the aerial version is no longer among the strongest meteor smashes in the game. The diagonal down variant deals less damage (13% → 12%) without compensation on knockback, hindering its KO power.
The diagonal down variant deals less damage (13% → 12%) without compensation on knockback, hindering its KO power. Substitute has more vibrant particle effects.
Substitute has more vibrant particle effects.
- Secret Ninja Attack:
 Greninja now turns into Ash-Greninja during its Final Smash.
Greninja now turns into Ash-Greninja during its Final Smash. Greninja and its opponents are no longer silhouetted during the attack.
Greninja and its opponents are no longer silhouetted during the attack. The final hit has considerably less knockback scaling (160 → 125), reducing the move's KO potential to the point where it is now weaker than the similar final smashes of Robin and Mii Brawler, both of which also deal less knockback now.
The final hit has considerably less knockback scaling (160 → 125), reducing the move's KO potential to the point where it is now weaker than the similar final smashes of Robin and Mii Brawler, both of which also deal less knockback now.
Update history
Greninja has received a mix of minor buffs and nerfs via game updates. Several glitches have also been fixed over time.
 A visual glitch with Greninja's screen KO has been fixed.
A visual glitch with Greninja's screen KO has been fixed.
 Down smash has a larger internal hitbox (Z offset: 0u → 0u-7u).
Down smash has a larger internal hitbox (Z offset: 0u → 0u-7u). Hydro Pump no longer instantly cancels Greninja's endlag when landing on a moving or slanted platform.
Hydro Pump no longer instantly cancels Greninja's endlag when landing on a moving or slanted platform.
 Water Shuriken deals less shield damage (0 → (-1.5 to -5.5)/-4.5 (uncharged/fully charged, hit 6)).
Water Shuriken deals less shield damage (0 → (-1.5 to -5.5)/-4.5 (uncharged/fully charged, hit 6)).
 Fixed an unknown glitch that resulted in Greninja sliding while shielding.
Fixed an unknown glitch that resulted in Greninja sliding while shielding.
 Greninja nows immediately descends when using down aerial after being launched, rather than air stalling.
Greninja nows immediately descends when using down aerial after being launched, rather than air stalling.
 Overall shield size has been increased by 1.206×.
Overall shield size has been increased by 1.206×.
 Pummel has a larger hitbox (5u → 6u), allowing it to connect more consistently.
Pummel has a larger hitbox (5u → 6u), allowing it to connect more consistently.
Moveset
- Greninja can crawl, wall cling, and wall jump.
For a gallery of Greninja's hitboxes, see here.
Note: All numbers are listed as base damage, without the 1v1 multiplier.
| Name | Damage | Description | ||
|---|---|---|---|---|
| Neutral attack | 2% | Two alternating palm thrusts followed by a double palm thrust that emits a small blast of water. If button mashed, it is instead followed by a series of knifehand strikes that emit blade-shaped water blasts that concludes with an outward knifehand strike that emits a wide blast of water. It can also be jab canceled, such as into forward tilt, down tilt and forward smash. | ||
| 2% | ||||
| 3% | ||||
| 0.5% (loop), 2% (last) | ||||
| Forward tilt | 7.3% | A hook kick which stops half way. It can be angled and can lock opponents. | ||
| Up tilt | 4.5% | Swings its tongue upwards. A good aerial combo starter and juggling tool due to its low knockback and somewhat disjointed hitbox. It can combo into itself at low percents and is a reliable way to connect into up aerial. | ||
| Down tilt | 4% | Does a downward hand sweep. It sends opponents at an upward angle, making it a versatile combo starter. Notably, it can confirm a KO into an up smash rather easily. | ||
| Dash attack | 8% | Does a sweep kick. Is arguably one of the best dash attacks in the game, as it launches opponents at an excellent angle for combos, making it one of Greninja's best combo starters. Reliably combos into back aerial at virtually any percent, and can set up up aerial strings or drag-down combos with up aerial. | ||
| Forward smash | 14% | An inward slash with a water kunai. Deals good knockback and has good range. However, it has notable ending lag. | ||
| Up smash | 5% (hit 1), 14% (hit 2 clean center), 11% (hit 2 clean sides), 10% (hit 2 late) | Two reverse gripped inward slashes with water kunai, similar to Sheik's up smash. Greninja's strongest finisher, especially when hit clean. Can be combo'd into from a down-tilt at specific percentages for a KO. | ||
| Down smash | 13% (kunai), 11% (arms) | Hits both sides with water kunai. Due to it sending opponents at an semi-spike angle and coming out on frame 11, it is a quick and effective way to set up an edge-guard situation. | ||
| Neutral aerial | 11% (clean), 6% (late) | Strikes a ninjutsu pose while emitting an exploding water bubble. Despite noticeable start-up lag for a neutral aerial(frame 12), it boasts great combo potential at low to mid percentages with its strong and weak hits and can KO confirm into up-smash at high percents with the weak hit. It can also KO at very high percents with its strong hit. | ||
| Forward aerial | 14% | Slashes with a water kunai. It has some start-up and suffers from high end lag, but it is a great tool in the neutral for spacing due to its disjointed hitbox and can be used for KOing. It is also safe on shield if spaced correctly. | ||
| Back aerial | 3% (hit 1), 2.5% (hit 2), 6% (hit 3) | Kicks backwards three times. It is Greninja's fastest aerial attack, although it is also one of the weakest aerials of its kind. However, this makes it a useful combo tool in return, as it can be followed up from a down throw, down tilt, as well as a dash attack. It can be a situational out-of-shield option if the opponent crosses-up on its shield. | ||
| Up aerial | 1.3% (hits 1-5), 3% (hit 6) | Does a upward corkscrew kick, similar to both Sheik's and Joker's up aerials. One of Greninja's best combo and KO tools, as it can juggle and KO effectively due to its great jumping prowess. It also allows for drag-down combos because it's multi-hit properties, although this requires precise timing to land it at the right time, as its final launching hit comes out too fast to set up drag-down combos otherwise. | ||
| Down aerial | 8% | A diving double foot stomp. It acts as a stall-then-fall and bounces off opponents. The clean hit meteor smashes opponents while the late hit sends the opponent upwards, allowing for some situational combos. | ||
| Grab | — | Grabs with a whirlpool. While its standing grab is slow, it is among the longest-reaching grabs in the game. | ||
| Pummel | 1% | Compresses target with water. Decent speed. | ||
| Forward throw | 3.5% (hit 1), 4.5% (throw) | Shoves the opponent forward. Can KO at high percentages near the edge. | ||
| Back throw | 9% | Greninja leans forward and flings the opponent backwards. Like forward throw, its decent knockback gives it good edgeguarding potential at high percentages. | ||
| Up throw | 5% | Tosses the opponent upwards. One of Greninja's most useful throws, as it can combo into a up tilt or up aerial at low and medium percents and can even KO at later percents. | ||
| Down throw | 5% | Slams the opponent onto the ground. It can combo into a down tilt, forward tilt, and dash attack at low percentages. It can combo into back aerial at medium percents and later into forward aerial as well at higher percentages with good timing. | ||
| Forward roll Back roll Spot dodge Air dodge |
— | — | ||
| Techs | — | — | ||
| Floor attack (front) Floor getups (front) |
8% | Sweep kicks around itself while getting up. | ||
| Floor attack (back) Floor getups (back) |
8% | Sweep kicks around itself while getting up. | ||
| Floor attack (trip) Floor getups (trip) |
8% | Sweep kicks around itself while getting up. | ||
| Edge attack Edge getups |
9% | Performs a roundhouse kick while climbing up. | ||
| Neutral special | Water Shuriken | 3%-10.8% (uncharged), 1.0% (fully charged looping hits), 9% (fully charged final hit) | Uses Water Shuriken, which can be charged. Depending on how long the move is charged, the shuriken will be larger and do more damage, however the speed and distance will decrease as a result. At full charge, it hits multiple times and can kill with a Shadow Sneak follow-up at low and medium percents. It is also a decent KOing option at higher percents. A fully charged water shuriken that is reflected at a higher speed will have trouble landing the final hit on Greninja because of the looping hits not moving Greninja far enough for it. | |
| Side special | Shadow Sneak | 10% (normal), 12% (reverse) | Disappears briefly, then preforms a forward kick or a drop kick (relative to the user's reappearance in relation to the enemy) to attack. The move activates when the special button is released. The way the shadow moves is relative to Greninja's position, and it can be moved further or closer to change how far Greninja teleports. While performing Shadow Sneak, Greninja cannot run, attack, grab, dodge or shield. However, it can walk slowly, jump and taunt. Has strong knockback and base knockback, which allows it to kill notably early when hitting the move offstage. | |
| Up special | Hydro Pump | 2% (per shot) | Uses Hydro Pump to propel itself in the inputted direction; it can be used twice. Each shot has a windbox effect that pushes opponents, making it a decent option for gimping predictable recoveries. | |
| Down special | Substitute | 14% (up or down), 11% (left or right) | Does a pose, and if anyone hits it while posing, Greninja will temporarily disappear, get replaced by a wooden log or a Substitute doll, and then appear behind the opponent and strike them. It deviates noticeably from other counters, as the attack itself can be angled in an inputted direction and launching the opponent in that direction (with the down input meteor smashing opponents, which makes it a good punish against reckless edgeguarders). | |
| Final Smash | Secret Ninja Attack | 6% (the mat), 50% (Total in the attack after mat) | Turns into Ash-Greninja and attacks the opponent with a mat. If an opponent is caught in the mat, Greninja will send them up into the air and strike the opponent repeatedly in midair with its kunai, before slamming them down with a final hit. | |
| Down taunt | 0.5% | While standing on one foot, Greninja holds out its hands, faces the screen, and summons small sprays of water. The sprays produce some knockback, though they're able to KO only at above 420%. A video showing the exact KO percentages at which each character can be KO'd can be found here. Unlike the rest of Greninja's taunts, this one cannot be cancelled (unless Shadow Sneak is being charged before using it). | ||
On-screen appearance
- Emerges from a Poké Ball, then performs a ninjutsu hand sign that emits a small burst of water from its hands.
Taunts
- Up Taunt: Stands upright, clasping its hands together before assuming a ninjutsu stance. The stance resembles one of its attack animations from the Pokémon series.
- Side Taunt: Shakes head from side to side, causing its tongue to whip out in the same directions. Particles of saliva fly off with each whip.
- Down Taunt: Poses with arms out and palms upward, and summons small sprays of water from them, which deal a small amount of damage.
Idle Poses
- Crosses arms over its body, then separates them with a flourish.
- Hunches over and assumes a ninjutsu stance.
Crowd cheer
| Cheer (English) | Cheer (Japanese/Chinese) | Cheer (Italian) | Cheer (Dutch) | Cheer (French) | |
|---|---|---|---|---|---|
| Cheer | |||||
| Description | Gre - ninja! | Ge - kkou -ga! | Gre - nin - ja! | Gre - ninja! | Am - phi - no - bi! |
Victory poses
- Left: Does a few hand seals with splashing water, and then a ninja pose. It resembles one of its attack animations in Pokémon X and Y.
- Up: Performs Double Team to briefly create three afterimages of itself.
- Right: Does a flip, lands in a spinning pose, and crosses its arms.
In competitive play
In the early metagame, players quickly noticed that Greninja had been buffed from Smash 4, with improved versatility and speed and, despite losing its footstool combos, gained a stronger combo game thanks to improved frame data on moves such as dash attack, up throw, down throw, and neutral air. Despite this, Greninja is not a very popular pick due to its high learning curve. Nevertheless, smashers such as Stroder, Venia, Jw, and Lea have proven that the character is a very viable pick, and Greninja has been solidified as a upper high-tier character.
Most historically significant players
Any number following the Smasher name indicates placement on the Fall 2019 PGRU, which recognizes the official top 50 players in the world in Super Smash Bros. Ultimate from July 13th, 2019 to December 15th, 2019.
See also: Category:Greninja professionals (SSBU)
Elexiao - One of the best Greninja players in Europe. Placed 1st at 4 Seasons Tournament: Winter 2020, 2nd at SEL 4: Crêpes Strikes Back, 5th at VCA 2019, 7th at Valhalla III, and 9th at Ultimate Fighting Arena 2019 with wins over players such as Oryon, Flow, and Tru4. Currently ranked 13th on the European Smash Rankings.
iStudying - One of the best Greninja players in Europe. Placed 1st at both The Ultimate Performance 3 and Heroes of Dutch Comic Con Winter Edition, 9th at both Ultimate Fighting Arena 2019 and Temple: Hermès Edition, and 13th at Valhalla III with wins over players such as Stroder Ame, quiK, and Space. Currently ranked 15th on the European Smash Rankings.
Jw - The best Greninja player in Canada. Placed 9th at Pound 2019, 13th at Shine 2019, 17th at both Get On My Level 2019 and The Big House 9, and 33rd at Frostbite 2020 with wins over players such as MkLeo, Mr. E, and Wishes. Currently ranked 1st on the Smash Canada Rankings Ultimate.
Lea (#21) - The best Greninja player in the world. Placed 5th at both Umebura SP 3 and Umebura SP 6, 7th at both 2GG: Kongo Saga and Kagaribi 4, and 9th at Frostbite 2019 with wins over players such as KEN, Raito, and Dabuz.
Oisiitofu - Placed 9th at both Sumabato SP 2 and Maesuma TOP 1, 13th at Sumabato SP 12, and 17th at both KVOxTSB 2019 and Sumabato SP 7 with wins over players such as Zackray, Atelier, and Nishiya. Currently ranked 86th on the Japan Player Rankings.
Regerets - The best Greninja player in the Philippines. Placed 3rd at Gamebookr's Mid-Year Smash Tournament and 7th at both Uprising 2019 and REV Major 2019 with wins over players such as Aluf, JJROCKETS, and PSI Force. Currently ranked 1st on the Filipino Power Rankings.
Somé - Placed 1st at TSC 11, 3rd at TSC 12, 7th at Sumabato SP 4, 9th at Umebura SP 6, and 13th at Umebura SP 4 with wins over players such as Jagaimo, Etsuji, and HIKARU. Currently ranked 21st on the Japan Player Rankings.
Stroder - One of the best Greninja players in the world. Placed 1st at Ascension VIII, 5th at Glitch 8 - Missingno, 9th at Mainstage, 13th at Shine 2019, and 25th at EVO 2019 with wins over players such as Tweek, Maister, and ESAM. Formerly ranked 29th on the Spring 2019 PGRU.
Tarik - One of the best Greninja players in Europe. Placed 1st at Calyptus Cup X: Powwer Up, 2nd at Smashwick 4, 7th at Syndicate 2019, 9th at Ultimate Fighting Arena 2019, and 25th at Glitch 8 - Missingno with wins over players such as ESAM, MVD, and Chag. Ranked 14th on the European Smash Rankings.
Venia - One of the best Greninja players in the United States but is currently banned from several tournaments. Placed 3rd at both Player's Ball Ultimate and Return to Yoshi's Island, 25th at Let's Make Big Moves, and 33rd at both The Big House 9 and GENESIS 7 with wins over Tweek, Dabuz, and Mr. E. Currently ranked 2nd on the New York City Ultimate Power Rankings.
Classic Mode: Your Turn, Greninja!
Greninja fights against characters that represent different types from the Pokémon games: for example, Charizard and Bowser represent the Fire type, while Mewtwo, Ness and Lucas represent the Psychic type.
| Round | Opponent | Stage | Music | Notes |
|---|---|---|---|---|
| 1 | Pokémon Stadium | Battle! (Elite Four) / Battle! (Solgaleo/Lunala) | Represents Fire-type. Charizard's Pokémon Trainer is absent. | |
| 2 | Pokémon Stadium 2 | Battle! (Steven) | Represents Electric-type. | |
| 3 | Pokémon Stadium | Battle! (Reshiram / Zekrom) | Represents Fighting-type. | |
| 4 | Pokémon Stadium | Battle! (Gladion) | Represents Grass-type. Ivysaur's Pokémon Trainer is absent. | |
| 5 | Pokémon Stadium 2 | Battle! (Dialga/Palkia) / Spear Pillar | Represents Psychic-type. | |
| 6 | Kalos Pokémon League | Battle! (Champion) - Pokémon X / Pokémon Y | Represents Water-type. Squirtle's Pokémon Trainer is absent. The CPU will be the | |
| Bonus Stage | ||||
| Final | Master Hand | Final Destination | Master Hand (Less than 7.0 intensity) Master Hand / Crazy Hand (Intensity 7.0 or higher) |
On intensity 7.0 and higher, Crazy Hand fights alongside Master Hand. |
Note: All rounds except the sixth round take place on Pokémon Stadium and Pokémon Stadium 2. If applicable, each stage will also shift to their appropriately-typed form at the earliest possible opportunity. (The stages remain in their default form in rounds 3 and 5, as none of the stages have Psychic or Fighting-themed forms.)
Credits roll after completing Classic Mode. Completing it as Greninja has Battle! (Trainer Battle) - Pokémon X / Pokémon Y accompany the credits.
Role in World of Light
Greninja was among the fighters that were summoned to fight the army of Master Hands.
During the opening cutscene, Greninja was present on the cliffside when Galeem unleashed his beams of light. Greninja leaped into the air to avoid one of the beams, which hit Lucario instead. Greninja was hit shortly after and vaporized, getting imprisoned by Galeem afterward along with the other fighters, sans Kirby. A puppet fighter cloned from Greninja is later seen alongside ones cloned from Fox, Samus, Link and other fighters.
Greninja was one of the many fighters that fell under Dharkon's control upon Galeem's first defeat, and it can be found in the Mysterious Dimension at The Dark Realm. It can be seen impeding the path, making it an obligatory unlock.
Greninja is later seen among several other fighters, making their last stand against Galeem and Dharkon. It also shows up in the bad ending where Galeem emerges victorious against Dharkon, witnessing Galeem engulf the world in light.
Fighter Battle
| No. | Image | Name | Type | Power | Stage | Music |
|---|---|---|---|---|---|---|
| 50 | Greninja | 10,600 | Kalos Pokémon League (Ω form) | Battle! (Trainer Battle) - Pokémon X / Pokémon Y |
Spirit
Greninja's fighter spirit can be obtained by completing Classic Mode. It is also available periodically for purchase in the shop for 300 Gold, but only after Greninja has been unlocked. Unlocking Greninja in World of Light allows the player to preview the spirit below in the Spirit List under the name "???". As a fighter spirit, it cannot be used in Spirit Battles and is purely aesthetic. Its fighter spirit has an alternate version that replaces it with its artwork in Ultimate.
In Spirit battles
As the main opponent
| Spirit | Battle parameters | Inspiration | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Image | Name | Series | Enemy Fighter(s) | Type | Power | Stage | Rules | Conditions | Music | Character |
| 154 | Winky | Donkey Kong Series | •Greninja |
1,700 | Mushroom Kingdom U | N/A | •The enemy deals damage when falling •The enemy has increased jump power |
Jungle Level (Brawl) | |||
| 199 | Zora | The Legend of Zelda Series | •Greninja |
1,800 | Great Bay | N/A | •The enemy's neutral special has increased power | Ocarina of Time Medley | |||
| 385 | Slippy Toad | Star Fox Series | •Greninja •Fox |
9,600 | Frigate Orpheon (hazards off) | N/A | •Defeat the main fighter to win •Timed battle (1:30) •The enemy tends to avoid conflict |
Corneria - Star Fox | |||
| 482 | Raikou, Entei, & Suicune | Pokémon Series | •Greninja •Incineroar •Pikachu |
9,900 | Suzaku Castle | •Hazard: Lava Floor | •The floor is lava | Pokémon Red / Pokémon Blue Medley | Suicune | ||
| 516 | Darkrai | Pokémon Series | •Greninja |
9,900 | Luigi's Mansion (Ω form) | •Item: Black Hole •Hazard: Slumber Floor |
•The floor is sleep-inducing •Only certain Pokémon will emerge from Poké Balls (Darkrai) |
Battle! (Team Galactic) | |||
| 770 | Metal Gear RAY | Metal Gear Solid Series | •Metal Greninja |
4,200 | Shadow Moses Island | •Item: Exploding Types | •Stamina battle •Explosion attacks aren't as effective against the enemy •The enemy is metal |
Yell "Dead Cell" | |||
| 893 | Shadow Man | Mega Man Series | •Greninja |
3,500 | Norfair (Battlefield form) | N/A | •The enemy's neutral special has increased power •Stamina battle •The enemy favors neutral specials |
Shadow Man Stage | |||
| 1,014 | Luka | Bayonetta Series | •Greninja |
3,800 | New Donk City Hall | •Temporary Invincibility | •The enemy becomes temporarily invincible when badly damaged | Riders Of The Light | |||
| 1,048 | Octoling Octopus | Splatoon Series | •Greninja Team |
3,900 | Moray Towers | N/A | •Timed battle (2:00) | Octoweaponry | |||
| 1,143 | Frog & Snake | Kaeru no Tame ni Kane wa Naru | •Greninja •King K. Rool |
3,600 | Dream Land GB (Castle Lololo interior) | •Assist Trophy Enemies (Sablé Prince) | •Hostile assist trophies will appear | Kirby Retro Medley (Castle Lololo) | Frog | ||
| 1,291 | Ninjara | ARMS | •Greninja |
3,600 | Suzaku Castle | •Item: Boomerang | •The enemy has increased move speed | Ninja College | |||
| •Mii Brawler | |||||||||||
- ^ This alternative occurs when the corresponding DLC has been purchased and downloaded.
Alternate costumes
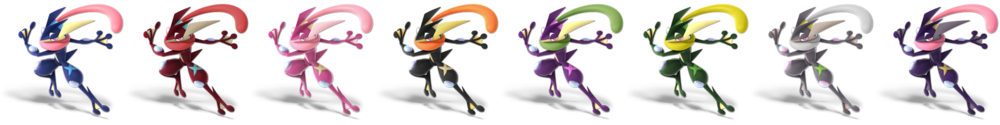
| |||||||

|

|

|

|

|

|

|

|
Gallery
Greninja coming to a halt on Kalos Pokémon League.
Charging Water Shuriken next to Ryu on Suzaku Castle.
Jumping on Battlefield.
With its Substitute Doll on Wuhu Island after tripping.
Performing Shadow Sneak on Luigi's Mansion.
Struck by Lucario on Pokémon Stadium 2.
Fighter Showcase Video
Trivia
- In the Pokémon series, Ash-Greninja is only obtainable as a male. The fact that Greninja transforms into Ash-Greninja for its Final Smash, Secret Ninja Attack, implies that Greninja is a male in Ultimate.
- Greninja's new character portrait resembles its air dodge animation.
- It also resembles Fox's character portrait from Super Smash Bros. 4 but with the arm and leg positions mirrored.
- Greninja's fighter number, 50, is the same as the number of its costume in Super Mario Maker. It shares this distinction with Inkling.
- Greninja, Ivysaur, Olimar, Little Mac, Ryu and Ken are the only characters to never appear as minions in any Spirit battles.
- Alongside Luigi, Greninja is one of two characters in Ultimate with a taunt that cannot be cancelled, due to the fact that their non-cancelable taunts have hitboxes.
- Greninja can also be unlocked immediately after clearing Classic Mode as Sheik, referencing their ninja-like traits and movements.
- Greninja appears slightly tilted in its damage meter compared to its character artwork. This distinction is shared with fellow Pokémon series character Incineroar.
- Coincidentally, both are final evolutions of starter Pokémon and both have Dark as their secondary type.
- Both are also found and unlocked in the Dark Realm in World of Light.
- Incineroar and Jigglypuff are the only Pokémon that are not encountered in Greninja's Classic Mode route.
- Oddly, Greninja does not vanish when performing a directional air dodge despite the sound effects playing. It shares this oddity with Rosalina & Luma and Palutena.
- In Ultimate, Greninja has a weight of 88, which almost matches its weight in Pokémon (in pounds), being 88.2 lbs.






























